Otimização em Sistemas de Energia Elétrica
Departamento de Engenharia Elétrica
Unidade 3
3.3. Método de Newton-Raphson
Solução de Equações Algébricas Não-lineares
As técnicas mais comumente utilizadas para solução de equações agébricas não-lineares são os métodos Gaus-Seidel, Newton-Raphson e Quase-Newton.
Inicialmente, será apresentando o método de Newton-Raphson unidimensional e, seguidamente, será extendido a equações $\small n$-dimensionais.
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
O método mais amplamente usado para resolver equações algébricas não-lineares simultâneas é o Método de Newton-Raphson.
Este método consiste em processo sucessivo de aproximações baseadas em uma estimativa inicial e o uso da expansão em séries de Taylor.
Considere a solução do da equação unidimensional dada por:
$\small f(x) = c$
Se $\small x^{(0)}$ é a aproximação inicial da solução, e $\small \Delta x^{(0)}$ é um pequeno desvio da solução correta, então:
$\small f(x^{(0)} + \Delta x^{(0)}) = c$
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
$\small f(x^{(0)} + \Delta x^{(0)}) = c$
Expandindo o lado esquerdo da anterior expressão em séries de Taylor em torno de $\small x^{(0)}$:
$\small f(x^{(0)}) + \left({\frac{df}{dx}}\right) ^{(0)}\Delta x^{(0)} + \frac{1}{2!}\left({\frac{d^2f}{dx^2}}\right)^{(0)}\Delta (x^{(0)})^2 + \cdots = c$
Assumindo que o erro $\small \Delta x^{(0)}$ seja muito pequeno, os termos de ordem superior podem ser desprezados, o que resulta em:
$\small \Delta c^{(0)} \simeq \left({\frac{df}{dx}}\right) ^{(0)}\Delta x^{(0)}$
Sendo:
$\small \Delta c^{(0)} = c - f(x^{(0)})$
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
$\small \Delta c^{(0)} \simeq \left({\frac{df}{dx}}\right) ^{(0)}\Delta x^{(0)}$
Sendo:
$\small \Delta c^{(0)} = c - f(x^{(0)})$
Adicionando $\small \Delta x^{(0)}$ à apriximação inicial, resultará na segunda aproximação:
$\small x^{(1)} = x^{(0)} + \frac{\Delta c^{(0)}}{\left({\frac{df}{dx}}\right)^{(0)}}$
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
$\small x^{(1)} = x^{(0)} + \frac{\Delta c^{(0)}}{\left({\frac{df}{dx}}\right)^{(0)}}$
O uso sucessivo da anterior expressão leva ao algoritmo de Newton-Raphson:
$\small \Delta c^{(k)} = c - f(x^{(k)})$
$\small \Delta x^{(k)} = \frac{\Delta c^{(k)}}{\left({\frac{df}{dx}}\right)^{(k)}}$
$\small x^{(k+1)} = x^{(k)} + \Delta x^{(k)}$
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
$\small \Delta c^{(k)} = c - f(x^{(k)})$
$\small \Delta x^{(k)} = \frac{\Delta c^{(k)}}{\left({\frac{df}{dx}}\right)^{(k)}}$
$\small x^{(k+1)} = x^{(k)} + \Delta x^{(k)}$
As anteriores expressões podem ser rearranjadas como:
$\small \Delta c^{(k)} = j^{(k)} \Delta x^{(k)}$
$\small j^{(k)} = \left({\frac{df}{dx}}\right)^{(k)}$
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
$\small \Delta c^{(k)} = j^{(k)} \Delta x^{(k)}$
$\small j^{(k)} = \left({\frac{df}{dx}}\right)^{(k)}$
A relação anterior demonstra que a equação não-linear $\small f(x) - c = 0$ é aproximada pela linha tangente à curva no ponto $\small x^{(k)}$. Assim, é obtida uma equação linear em termos de pequenas mudanças na variável.
A interseção da linha tangente no ponto $\small x^{(k)}$ com o eixo $\small x$ resulta em $\small x^{(k + 1)}$. Esta ideia é demonstrada graficamente no exemplo a seguir.
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson - Exemplo 3.3.1
Usar o Método Newton-Raphson, considerando como solução inicial $\small x^{(0)} = 6$, para determinar a raiz da seguinte equação:
$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$
$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$
A derivada de $\small f(x)$ é:
$\small \frac{df(x)}{dx} = 3x^2 - 12x + 9$
Na primeira iteração, $\Delta c^{(0)}$ é:
$\small \Delta c^{(0)} = c - f(x^{(0)}) = 0 - 50 = -50$
$\small \left({\frac{df}{dx}}\right)^{(0)} = 45$
$\small \Delta x^{(0)} = \frac{\Delta c^{(0)}}{\left({\frac{df}{dx}}\right)^{(0)}} = \frac{-50}{45} = -1,1111$
Assim, o resultado no final da primeira iteração é:
$\small x^{(1)} = x^{(0)} + \Delta x^{(0)} = 6 - 1,1111 = 4,8889$
Nas iterações subsequentes resultam em:
$\small x^{(2)} = x^{(1)} + \Delta x^{(1)} = 4,8889 - \frac{13,4431}{22,037} = 4,2789$
$\small x^{(3)} = x^{(2)} + \Delta x^{(2)} = 4,2789 - \frac{2,9981}{12,5797} = 4,0405$
$\small x^{(4)} = x^{(3)} + \Delta x^{(3)} = 4,0405 - \frac{0,3748}{9,4914} = 4,0011$
$\small x^{(5)} = x^{(4)} + \Delta x^{(4)} = 4,0011 - \frac{0,0095}{9,0126} = 4,0000$
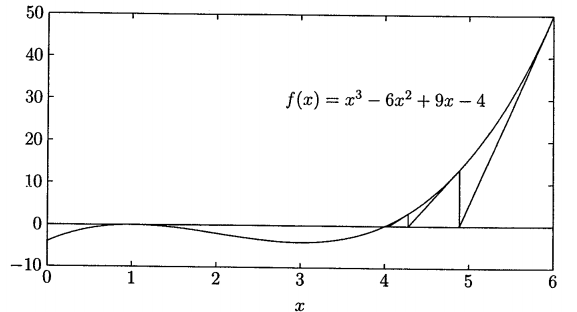
Pode ser observado que o Método de Newton-Raphson converge consideravelmente mais rapidamente que o Método Gauss-Seidel.
O Método de Newton-Raphson pode convergir a uma raiz diferente da esperada ou então divergir se a aproximação inicial não está o suficientemente próxima da raiz.
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
Considere agora o seguinte conjunto $\small n$ dimensional de equações:
$\small \begin{array}{*{20}{c}} {{{\left( {{f_1}} \right)}^{(0)}} + {{\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}}} \right)}^{(0)}}\Delta x_1^{(0)} + {{\left( {\frac{{\partial {f_1}}}{{\partial {x_2}}}} \right)}^{(0)}}\Delta x_2^{(0)} + \cdots + {{\left( {\frac{{\partial {f_1}}}{{\partial {x_n}}}} \right)}^{(0)}}\Delta x_n^{(0)} = {c_1}}\\ {{{\left( {{f_2}} \right)}^{(0)}} + {{\left( {\frac{{\partial {f_2}}}{{\partial {x_1}}}} \right)}^{(0)}}\Delta x_1^{(0)} + {{\left( {\frac{{\partial {f_2}}}{{\partial {x_2}}}} \right)}^{(0)}}\Delta x_2^{(0)} + \cdots + {{\left( {\frac{{\partial {f_2}}}{{\partial {x_n}}}} \right)}^{(0)}}\Delta x_n^{(0)} = {c_2}}\\ \vdots \\ {{{\left( {{f_n}} \right)}^{(0)}} + {{\left( {\frac{{\partial {f_n}}}{{\partial {x_1}}}} \right)}^{(0)}}\Delta x_1^{(0)} + {{\left( {\frac{{\partial {f_n}}}{{\partial {x_2}}}} \right)}^{(0)}}\Delta x_2^{(0)} + \cdots + {{\left( {\frac{{\partial {f_n}}}{{\partial {x_n}}}} \right)}^{(0)}}\Delta x_n^{(0)} = {c_n}} \end{array}$
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
Ou na forma matricial:
$\scriptsize \left[ {\begin{array}{*{20}{c}} {{c_1} - {{\left( {{f_1}} \right)}^{(0)}}}\\ {{c_2} - {{\left( {{f_2}} \right)}^{(0)}}}\\ \vdots \\ {{c_n} - {{\left( {{f_n}} \right)}^{(0)}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}}} \right)}^{(0)}}}&{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_{2}}}}} \right)}^{(0)}}}& \cdots &{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_n}}}} \right)}^{(0)}}}\\ {{{\left( {\frac{{\partial {f_2}}}{{\partial {x_1}}}} \right)}^{(0)}}}&{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_{2}}}}} \right)}^{(0)}}}& \cdots &{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_n}}}} \right)}^{(0)}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{{\left( {\frac{{\partial {f_n}}}{{\partial {x_1}}}} \right)}^{(0)}}}&{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_{2}}}}} \right)}^{(0)}}}& \cdots &{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_n}}}} \right)}^{(0)}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta x_1^{(0)}}\\ {\Delta x_2^{(0)}}\\ \vdots \\ {\Delta x_n^{(0)}} \end{array}} \right]$
Em forma compacta, pode ser escrito como:
$\small \Delta C^{(k)} = J^{(k)} \Delta X^{(k)}$
ou
$\small \Delta X^{(k)} = \left[{ J^{(k)} }\right] ^{-1} \Delta C^{(k)} $
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
$\small \Delta X^{(k)} = \left[{ J^{(k)} }\right] ^{-1} \Delta C^{(k)} $
A atualização das variáveis usando o Método de Newton-Raphson, para o sistema $\small n$ dimensional, fica então:
$\small X^{(k + 1)} = X^{(k)} + \Delta X^{(k)} $
Sendo:
$\tiny \Delta {X^{(k)}} = \left[ {\begin{array}{*{20}{c}} {\Delta x_1^{(k)}}\\ {\Delta x_2^{(k)}}\\ \vdots \\ {\Delta x_n^{(k)}} \end{array}} \right];{\rm{ }}\Delta {C^{(k)}} = \left[ {\begin{array}{*{20}{c}} {{c_1} - {{\left( {{f_1}} \right)}^{(k)}}}\\ {{c_2} - {{\left( {{f_2}} \right)}^{(k)}}}\\ \vdots \\ {{c_n} - {{\left( {{f_n}} \right)}^{(k)}}} \end{array}} \right];{\rm{ }}{J^{(k)}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_n}}}} \right)}^{(k)}}}\\ {{{\left( {\frac{{\partial {f_2}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_n}}}} \right)}^{(k)}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{{\left( {\frac{{\partial {f_n}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_n}}}} \right)}^{(k)}}} \end{array}} \right]$
Solução de Equações Algébricas Não-lineares - Método Newton-Raphson
$\tiny \Delta {X^{(k)}} = \left[ {\begin{array}{*{20}{c}} {\Delta x_1^{(k)}}\\ {\Delta x_2^{(k)}}\\ \vdots \\ {\Delta x_n^{(k)}} \end{array}} \right];{\rm{ }}\Delta {C^{(k)}} = \left[ {\begin{array}{*{20}{c}} {{c_1} - {{\left( {{f_1}} \right)}^{(k)}}}\\ {{c_2} - {{\left( {{f_2}} \right)}^{(k)}}}\\ \vdots \\ {{c_n} - {{\left( {{f_n}} \right)}^{(k)}}} \end{array}} \right];{\rm{ }}{J^{(k)}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_n}}}} \right)}^{(k)}}}\\ {{{\left( {\frac{{\partial {f_2}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_n}}}} \right)}^{(k)}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{{\left( {\frac{{\partial {f_n}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_n}}}} \right)}^{(k)}}} \end{array}} \right]$
$\small J^{(k)}$ é chamada de Matriz Jacobiana. Os elementos desta matriz são as derivadas parciais avaliadas no ponto $\small X^{(k)}$.
É assumido que $\small J^{(k)}$ tem inversa em cada iteração.
O Método de Newton-Raphson, quando aplicado a um conjunto de equações não-lineares, reduz o problema à resolução de um sistema de equações lineares.
Exemplo 3.3.2: Método de Newton-Raphson (Problema Multivariável)
Usar o Método de Newton-Raphson para obter uma solução para o sistema linear $\small A X = b$, sendo:
\[ \small A = \left[ {\begin{array}{*{20}{c}} \small 5 & 1 & 1\\ \small 3 & 4 & 1\\ \small 3 & 3 & 6 \end{array}} \right]; \ \ b = \left[ {\begin{array}{*{20}{c}} \small 5\\ \small 6\\ \small 0 \end{array}} \right],\]
a partir do ponto $ \small {X^{(0)}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}} \right]$ e com uma precisão $ \small \epsilon = 10^{-2}$.
Sistema de funções correspondente:
$\small \begin{array}{*{20}{c}} \small f_1(x_1, x_2, x_3) & = & 5x_1 & + & x_2 & + & x_3 & - & 5 & = & 0 \\ \small f_2(x_1, x_2, x_3) & = & 3x_1 & + & 4x_2 & + & x_3 & - & 6 & = & 0\\ \small f_3(x_1, x_2, x_3) & = & 3x_1 & + & 3x_2 & + & 6x_3 & & & = & 0\\ \end{array} $
Formulação para aplicação do método:
$\tiny X = \left[ {\begin{array}{*{20}{c}} { x_1}\\ { x_2}\\ { x_3} \end{array}} \right];{\rm{ }} F(X) = \left[ {\begin{array}{*{20}{c}} {{{ {{f_1(X)}} }}}\\ { {{ {{f_2(X)}} }}}\\ { {{ {{f_3(X)}} }}} \end{array}} \right];{\rm{ }}{\nabla F(X)} = J(X) = \left[ {\begin{array}{*{20}{c}} 5 & 1 & 1\\ 3 & 4 & 1\\ 3 & 3 & 6\\ \end{array}} \right];{\rm{ }}{J(X)^{-1}} = \frac{1}{29} \left[ {\begin{array}{*{20}{c}} 7 & -1 & -1\\ -5 & 9 & -2/3\\ -1 & -4 & 17/3\\ \end{array}} \right]$
Lembrando que:
$\small \Delta X^{(k)} = \left[{ J^{(k)} }\right] ^{-1} F^{(k)} $
$\small X^{(k + 1)} = X^{(k)} + \Delta X^{(k)} $
Formulação para aplicação do método:
$\tiny X = \left[ {\begin{array}{*{20}{c}} { x_1}\\ { x_2}\\ { x_3} \end{array}} \right];{\rm{ }} F(X) = \left[ {\begin{array}{*{20}{c}} {{{ {{f_1(X)}} }}}\\ { {{ {{f_2(X)}} }}}\\ { {{ {{f_3(X)}} }}} \end{array}} \right];{\rm{ }}{\nabla F(X)} = J(X) = \left[ {\begin{array}{*{20}{c}} 5 & 1 & 1\\ 3 & 4 & 1\\ 3 & 3 & 6\\ \end{array}} \right];{\rm{ }}{J(X)^{-1}} = \frac{1}{29} \left[ {\begin{array}{*{20}{c}} 7 & -1 & -1\\ -5 & 9 & -2/3\\ -1 & -4 & 17/3\\ \end{array}} \right]$
$\small \Delta X^{(k)} = \left[{ J^{(k)} }\right] ^{-1} F^{(k)} $
$\small X^{(k + 1)} = X^{(k)} + \Delta X^{(k)} $
Primeira iteração ($\small k = 0$):
$\small \Delta X^{(0)} = \frac{1}{29} \left[ {\begin{array}{*{20}{c}} 7 & -1 & -1\\ -5 & 9 & -2/3\\ -1 & -4 & 17/3\\ \end{array}} \right] \left[ {\begin{array}{*{20}{c}} -5\\ -6\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1\\ 1\\ -1 \end{array}} \right]$
$\small X^{(1)} = X^{(0)} + \Delta X^{(0)} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 1\\ 1\\ -1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1\\ 1\\ -1 \end{array}} \right]$
Segunda iteração ($\small k = 1$):
$\small \Delta X^{(1)} = \frac{1}{29} \left[ {\begin{array}{*{20}{c}} 7 & -1 & -1\\ -5 & 9 & -2/3\\ -1 & -4 & 17/3\\ \end{array}} \right] \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}} \right]$
$\small X^{(2)} = X^{(1)} + \Delta X^{(1)} = \left[ {\begin{array}{*{20}{c}} 1\\ 1\\ -1\\ \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1\\ 1\\ -1 \end{array}} \right]$
Verificação do critério de parada:
$ \small \frac{{\left\| {{x^{(2)}} - {x^{(1)}}} \right\|}}{{\left\| {{x^{(2)}}} \right\|}} = \frac{{\left\| {0} \right\|}}{{\left\| {1} \right\|}} = 0 < {10^{ - 2}}$ $\small \rightarrow$ Convergiu!
Otimização em Sistemas de Energia Elétrica
Departamento de Engenharia Elétrica

