Otimização em Sistemas de Energia Elétrica
Departamento de Engenharia Elétrica
Unidade 3
3.2. Método de Gauss-Seidel
Solução de Equações Algébricas Não-lineares
As técnicas mais comumente utilizadas para solução de equações agébricas não-lineares são os métodos Gauss-Seidel, Newton-Raphson e Quase-Newton.
Inicialmente, será apresentando o método Gauss-Seidel unidimensional e, seguidamente, será extendido a equações $\small n$-dimensionais.
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
O método Gauss-Seidel também é conhecido como "Método de deslocamentos sucessivos".
Para ilustrar a técnica, considere a solução da equação não-linear dada por:
$\small f(x) = 0$
A anterior função é rearanjada e escrita como:
$\small x = g(x)$
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
Se $\small x^{(k)}$ é uma aproximação inicial da variável $\small x$, então é formada a seguinte sequência iterativa:
$\small x^{(k+1)} = g \left({ x^{(k)} }\right) $
A solução é obtida quando a diferença entre o valor absoluto de uma iteração sucessiva é menor que uma tolerância especificada $\small \epsilon$, isto é:
$\small | x^{(k+1)} - x^{(k)} | \leq \epsilon$
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel - Exemplo 3.2.1
Usar o Método Gauss-Seidel, considerando como solução inicial $\small x^{(0)} = 2$ (no intervalo 1 a 4), para determinar a raiz da seguinte equação:
$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$
$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$
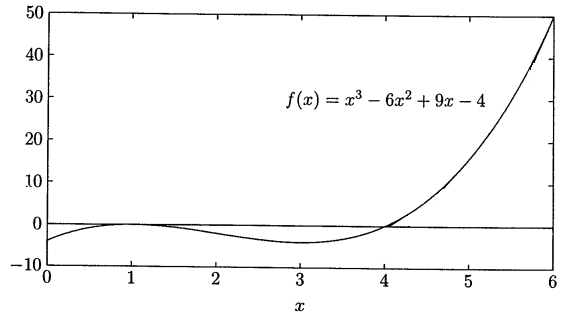
$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$
Resolvendo para $\small x$, a expressão anterior é escrita como:
$\small x = -\frac{1}{9}x^3 + \frac{6}{9}x^2 + \frac{4}{9} $
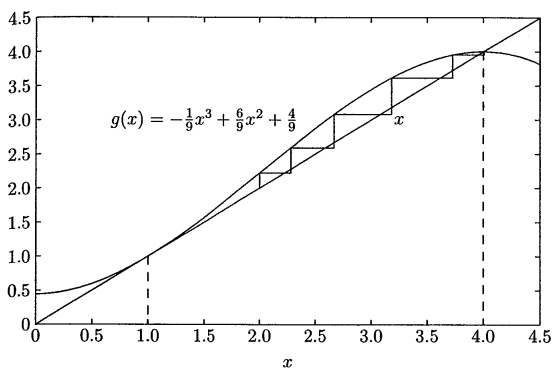
$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$
Resolvendo para $\small x$, a expressão anterior é escrita como:
$\small x = -\frac{1}{9}x^3 + \frac{6}{9}x^2 + \frac{4}{9} $
A primeira iteração é:
$\small x^{(1)} = g(x^{(0)}) = g(2) = -\frac{1}{9}2^3 + \frac{6}{9}2^2 + \frac{4}{9} = 2,2222$
A segunda iteração é:
$\small x^{(2)} = g(x^{(1)}) = g(2.2222) = -\frac{1}{9}2.2222^3 + \frac{6}{9}2.2222^2 + \frac{4}{9} = 2,5173$
As subsequentes iterações resultam em 2.8966, 3.3376, 3.7398, 3.9568, 3.9988 e 4.0000 . O processo é repetido até que a mudança na variável esteja dentro da tolerância desejada.
Pode ser observado que o Método Gauss-Seidel precisa de muitas iterações para alcançar a precisão desejada. Além disso, não há garantia de convergência.
Neste exemplo, dado que a solução inicial ($\small x^{(0)} = 2$) está em uma região "fechada", a solução converge em forma de "zigzag" a uma das raízes.
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
Considerando agora um sistema de $\small n$ equações não-lineares com $\small n$ incógnitas:
$\small \begin{array}{*{20}{c}} {{f_1}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_1}}\\ {{f_2}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_2}}\\ \vdots \\ {{f_n}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_n}} \end{array} $
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
$\small \begin{array}{*{20}{c}} {{f_1}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_1}}\\ {{f_2}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_2}}\\ \vdots \\ {{f_n}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_n}} \end{array} $
Resolvendo para cada equação, as funções acima são rearranjadas e escritas como:
$\small \begin{array}{*{20}{c}} {{x_1} = c_1 + g_1\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)}\\ {{x_2} = c_2 + g_2\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)}\\ \vdots \\ {{x_n} = c_n + g_n\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)} \end{array} $
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
$\small \begin{array}{*{20}{c}} {{x_1} = c_1 + g_1\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)}\\ {{x_2} = c_2 + g_2\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)}\\ \vdots \\ {{x_n} = c_n + g_n\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)} \end{array} $
O processo iterativo é iniciado assumindo uma solução aproximada para cada variável independentemente ($\small x_1^{(0)}$, $\small x_2^{(0)}$, $\small \cdots$, $\small x_n^{(0)}$).
A solução do sistema de equações anterior resulta em uma nova aproximação ($\small x_1^{(1)}$, $\small x_2^{(1)}$, $\small \cdots$, $\small x_n^{(1)}$).
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
No método Gauss-Seidel, os valores atualizados das variáveis calculadas nas anteriores equações são imediatamente usados na solução das equações subsequentes.
No final de cada iteração, os valores calculados de todas as variáveis são comparados com seus correspondentes valores prévios. Se todas as mudanças nas variáveis estão dentro da tolerância especificada, a solução tem convergido.
A velocidade de convergência pode ser incrementada usando um fator de aceleração $\small \alpha$, e a iteração subsequente fica:
$\small x_i^{(k + 1)} = x_i^{(k)} + \alpha ( x_{i,calc}^{(k + 1)} - x_i^{(k)})$
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
Retomando o sistema de $\small n$ equações não-lineares com $\small n$ incógnitas:
$\small \begin{array}{*{20}{c}} {{f_1}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_1}}\\ {{f_2}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_2}}\\ \vdots \\ {{f_n}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_n}} \end{array} $
ou
$\small \begin{array}{*{20}{c}} {a_{11} x_1 + a_{12} x_2 + a_{13} x_3 + \cdots a_{1n} x_n = {c_1}}\\ {a_{21} x_1 + a_{22} x_2 + a_{23} x_3 + \cdots a_{2n} x_n = {c_2}}\\ \vdots \\ {a_{n1} x_1 + a_{n2} x_2 + a_{n3} x_3 + \cdots a_{nn} x_n = {c_n}} \end{array} $
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
$\small \begin{array}{*{20}{c}} {a_{11} x_1 + a_{12} x_2 + a_{13} x_3 + \cdots a_{1n} x_n = {c_1}}\\ {a_{21} x_1 + a_{22} x_2 + a_{23} x_3 + \cdots a_{2n} x_n = {c_2}}\\ \vdots \\ {a_{n1} x_1 + a_{n2} x_2 + a_{n3} x_3 + \cdots a_{nn} x_n = {c_n}} \end{array} $
Resolvendo para $\small x_1$, $\small x_2$, $\small \cdots$, $\small x_n$, tem-se que:
$\small \begin{array}{*{20}{c}} {x_1 = \frac{c_1}{a_{11}} + \left({ - \frac{a_{12}}{a_{11}} x_2 - \frac{a_{13}}{a_{11}} x_3 - \cdots - \frac{a_{1n}}{a_{11}} x_n }\right)}\\ {x_2 = \frac{c_2}{a_{22}} + \left({ - \frac{a_{21}}{a_{22}} x_1 - \frac{a_{23}}{a_{22}} x_3 - \cdots - \frac{a_{2n}}{a_{22}} x_n }\right)}\\ \vdots \\ {x_n = \frac{c_n}{a_{nn}} + \left({ - \frac{a_{n1}}{a_{nn}} x_1 - \frac{a_{n2}}{a_{nn}} x_2 - \cdots - \frac{a_{nn-1}}{a_{nn}} x_{n-1} }\right)} \end{array} $
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
$\scriptsize \begin{array}{*{20}{c}} {x_1 = \frac{c_1}{a_{11}} + \left({ - \frac{a_{12}}{a_{11}} x_2 - \frac{a_{13}}{a_{11}} x_3 - \cdots - \frac{a_{1n}}{a_{11}} x_n }\right)}\\ {x_2 = \frac{c_2}{a_{22}} + \left({ - \frac{a_{21}}{a_{22}} x_1 - \frac{a_{23}}{a_{22}} x_3 - \cdots - \frac{a_{2n}}{a_{22}} x_n }\right)}\\ \vdots \\ {x_n = \frac{c_n}{a_{nn}} + \left({ - \frac{a_{n1}}{a_{nn}} x_1 - \frac{a_{n2}}{a_{nn}} x_2 - \cdots - \frac{a_{nn-1}}{a_{nn}} x_{n-1} }\right)} \end{array} $
Na primeira iteração, tem-se que:
$\scriptsize \begin{array}{*{20}{c}} {x_1^{(1)} = \frac{c_1}{a_{11}} + \left({ - \frac{a_{12}}{a_{11}} x_2^{(0)} - \frac{a_{13}}{a_{11}} x_3^{(0)} - \cdots - \frac{a_{1n}}{a_{11}} x_n^{(0)} }\right)}\\ {x_2^{(1)} = \frac{c_2}{a_{22}} + \left({ - \frac{a_{21}}{a_{22}} x_1^{(1)} - \frac{a_{23}}{a_{22}} x_3^{(0)} - \cdots - \frac{a_{2n}}{a_{22}} x_n^{(0)} }\right)}\\ \vdots \\ {x_n^{(1)} = \frac{c_n}{a_{nn}} + \left({ - \frac{a_{n1}}{a_{nn}} x_1^{(1)} - \frac{a_{n2}}{a_{nn}} x_2^{(1)} - \cdots - \frac{a_{nn-1}}{a_{nn}} x_{n-1}^{(1)} }\right)} \end{array} $
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
$\scriptsize \begin{array}{*{20}{c}} {x_1^{(1)} = \frac{c_1}{a_{11}} + \left({ - \frac{a_{12}}{a_{11}} x_2^{(0)} - \frac{a_{13}}{a_{11}} x_3^{(0)} - \cdots - \frac{a_{1n}}{a_{11}} x_n^{(0)} }\right)}\\ {x_2^{(1)} = \frac{c_2}{a_{22}} + \left({ - \frac{a_{21}}{a_{22}} x_1^{(1)} - \frac{a_{23}}{a_{22}} x_3^{(0)} - \cdots - \frac{a_{2n}}{a_{22}} x_n^{(0)} }\right)}\\ \vdots \\ {x_n^{(1)} = \frac{c_n}{a_{nn}} + \left({ - \frac{a_{n1}}{a_{nn}} x_1^{(1)} - \frac{a_{n2}}{a_{nn}} x_2^{(1)} - \cdots - \frac{a_{nn-1}}{a_{nn}} x_{n-1}^{(1)} }\right)} \end{array} $
Na iteração $\small k + 1$, tem-se que:
$\scriptsize \begin{array}{*{20}{c}} {x_1^{(k + 1)} = \frac{c_1}{a_{11}} + \left({ - \frac{a_{12}}{a_{11}} x_2^{(k)} - \frac{a_{13}}{a_{11}} x_3^{(k)} - \cdots - \frac{a_{1n}}{a_{11}} x_n^{(k)} }\right)}\\ {x_2^{(k + 1)} = \frac{c_2}{a_{22}} + \left({ - \frac{a_{21}}{a_{22}} x_1^{(k + 1)} - \frac{a_{23}}{a_{22}} x_3^{(k)} - \cdots - \frac{a_{2n}}{a_{22}} x_n^{(k)} }\right)}\\ \vdots \\ {x_n^{(k + 1)} = \frac{c_n}{a_{nn}} + \left({ - \frac{a_{n1}}{a_{nn}} x_1^{(k + 1)} - \frac{a_{n2}}{a_{nn}} x_2^{(k + 1)} - \cdots - \frac{a_{nn-1}}{a_{nn}} x_{n-1}^{(k + 1)} }\right)} \end{array} $
Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel
$\small \begin{array}{*{20}{c}} {x_1^{(k + 1)} = \frac{c_1}{a_{11}} + \left({ - \frac{a_{12}}{a_{11}} x_2^{(k)} - \frac{a_{13}}{a_{11}} x_3^{(k)} - \cdots - \frac{a_{1n}}{a_{11}} x_n^{(k)} }\right)}\\ {x_2^{(k + 1)} = \frac{c_2}{a_{22}} + \left({ - \frac{a_{21}}{a_{22}} x_1^{(k + 1)} - \frac{a_{23}}{a_{22}} x_3^{(k)} - \cdots - \frac{a_{2n}}{a_{22}} x_n^{(k)} }\right)}\\ \vdots \\ {x_n^{(k + 1)} = \frac{c_n}{a_{nn}} + \left({ - \frac{a_{n1}}{a_{nn}} x_1^{(k + 1)} - \frac{a_{n2}}{a_{nn}} x_2^{(k + 1)} - \cdots - \frac{a_{nn-1}}{a_{nn}} x_{n-1}^{(k + 1)} }\right)} \end{array} $
Assim, para $\small i = 1, 2, 3, \cdots, n$, na iteração $\small k + 1$, tem-se a seguinte expressão geral para o cálculo de $\small x_i^{(k + 1)}$:
$\small x_i^{(k + 1)} = \frac{c_i}{a_{ii}} - \sum\limits_{j = 1}^{i - 1} { \frac{a_{ij}}{a_{ii}} x_j^{(k + 1)} } - \sum\limits_{j = i + 1}^{n} { \frac{a_{ij}}{a_{ii}} x_j^{(k)} } $
Exemplo 3.2.2: Método de Gauss-Seidel (Problema Multivariável)
Usar o Método de Gauss-Seidel Gau para obter uma solução para o sistema linear $\small A X = b$, sendo:
\[ \small A = \left[ {\begin{array}{*{20}{c}} \small 5 & 1 & 1\\ \small 3 & 4 & 1\\ \small 3 & 3 & 6 \end{array}} \right]; \ \ b = \left[ {\begin{array}{*{20}{c}} \small 5\\ \small 6\\ \small 0 \end{array}} \right],\]
a partir do ponto $ \small {X^{(0)}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}} \right]$ e com uma precisão $ \small \epsilon = 10^{-2}$.
Sistema de equações correspondente:
$\small \begin{array}{*{20}{c}} \small 5x_1 & + & x_2 & + & x_3 & = & 5\\ \small 3x_1 & + & 4x_2 & + & x_3 & = & 6\\ \small 3x_1 & + & 3x_2 & + & 6x_3 & = & 0\\ \end{array} $
Normalização das variáveis em cada equação:
$\small \begin{array}{*{20}{c}} \small x_1 & + & 0,2x_2 & + & 0,2x_3 & = & 1\\ \small 0,75x_1 & + & x_2 & + & 0,25x_3 & = & 1,5\\ \small 0,5x_1 & + & 0,5x_2 & + & x_3 & = & 0\\ \end{array} $
Obtenção das equações $\small g_i\left( {{x_1},{x_2} ,{x_3}} \right)$:
$\small \begin{array}{*{20}{c}} \small x_1 & = & - 0,2x_2 & - 0,2x_3 & + & 1\\ \small x_2 & = & - 0,75x_1 & - 0,25x_3 & + & 1,5\\ \small x_3 & = & - 0,5x_1 & - 0,5x_2 \\ \end{array} $
Equações $\small g_i\left( {{x_1},{x_2} ,{x_3}} \right)$:
$\small \begin{array}{*{20}{c}} \small x_1 & = & - 0,2x_2 & - 0,2x_3 & + & 1\\ \small x_2 & = & - 0,75x_1 & - 0,25x_3 & + & 1,5\\ \small x_3 & = & - 0,5x_1 & - 0,5x_2 \\ \end{array} $
Lembrando a expressão geral para o cálculo de $\small x_i^{(k + 1)}$:
$\small x_i^{(k + 1)} = \frac{c_i}{a_{ii}} - \sum\limits_{j = 1}^{i - 1} { \frac{a_{ij}}{a_{ii}} x_j^{(k + 1)} } - \sum\limits_{j = i + 1}^{n} { \frac{a_{ij}}{a_{ii}} x_j^{(k)} } $
Tem-se que:
$\small \begin{array}{*{20}{c}} \small x_1^{(k + 1)} & = & - 0,2x_2^{(k)} & - 0,2x_3^{(k)} & + & 1\\ \small x_2^{(k + 1)} & = & - 0,75x_1^{(k)} & - 0,25x_3^{(k)} & + & 1,5\\ \small x_3^{(k + 1)} & = & - 0,5x_1^{(k)} & - 0,5x_2^{(k)} \\ \end{array} $
$\small \begin{array}{*{20}{c}} \small x_1^{(k + 1)} & = & - 0,2x_2^{(k)} & - 0,2x_3^{(k)} & + & 1\\ \small x_2^{(k + 1)} & = & - 0,75x_1^{(k)} & - 0,25x_3^{(k)} & + & 1,5\\ \small x_3^{(k + 1)} & = & - 0,5x_1^{(k)} & - 0,5x_2^{(k)} \\ \end{array} $
Primeira iteração ($\small k = 0$):
$\scriptsize \begin{array}{*{20}{c}} \scriptsize x_1^{(1)} & = & - 0,2x_2^{(0)} - 0,2x_3^{(0)} + 1 & = & -0,2(0) -0,2(0) + 1 & = & 1\\ \scriptsize x_2^{(1)} & = & - 0,75x_1^{(1)} - 0,25x_3^{(0)} + 1,5 & = & -0,75(1) -0,25(0) + 1,5 & = & 0,75\\ \scriptsize x_3^{(1)} & = & - 0,5x_1^{(1)} - 0,5x_2^{(1)} & = & - 0,5(1) -0,5(0,75) & = & -0,875 \\ \end{array} $
Continuando com o processo iterativo:
$ \scriptsize \begin{array}{||c||c|c|c|c|c||} \hline \hline k & 0 & 1 & 2 & 3 & 4 \\ \hline x_1^{(k )} & 0 & 1 & 1,025 & 1,0075 & 1,0016 \\ \hline x_2^{(k )} & 0 & 0,75 & 0,95 & 0,9913 & 0,9987 \\ \hline x_3^{(k )} & 0 & -0,875 & -0,9875 & -0,9994 & -1,0002 \\ \hline \end{array} $
$ \scriptsize \begin{array}{||c||c|c|c|c|c||} \hline \hline k & 0 & 1 & 2 & 3 & 4 \\ \hline x_1^{(k )} & 0 & 1 & 1,025 & 1,0075 & 1,0016 \\ \hline x_2^{(k )} & 0 & 0,75 & 0,95 & 0,9913 & 0,9987 \\ \hline x_3^{(k )} & 0 & -0,875 & -0,9875 & -0,9994 & -1,0002 \\ \hline \end{array} $
Verificação do critério de parada:
$ \small \frac{{\left\| {{x^{(4)}} - {x^{(3)}}} \right\|}}{{\left\| {{x^{(4)}}} \right\|}} = \frac{{\left\| {0,0074} \right\|}}{{\left\| {1,0016} \right\|}} = 0,0074 < {10^{ - 2}}$ $\small \rightarrow$ Convergiu!
Otimização em Sistemas de Energia Elétrica
Departamento de Engenharia Elétrica

