Otimização em Sistemas de Energia Elétrica
Departamento de Engenharia Elétrica
Unidade 4
4.3. AMPL
A Mathematical Programming Language
Introdução
Linguagem de alto nível para descrever problemas de programação matemática.
AMPL permite que um modelo de programação matemática seja especificado independentemente dos dados usados para uma instância específica do modelo.
A linguagem usada por AMPL para descrever problemas de programação matemática é bastante aproxiamada da linguagem usada pelos humanos para descrever modelos matemáticos. Por esse motivo, os programadores podem passar mais tempo melhorando o modelo e menos tempo em detalhes de manipulação de dados e implementação de métodos para resolver problemas.
Introdução
AMPL funciona como uma interface: o modelo e a entrada são colocados de forma que podem ser lidos por um pacote de otimização ou solver.
O solver procura a solução ótima do problema lendo a informação fornecida por AMPL e aplicando um algoritmo apropriado.
O solver entrega a solução em formato de texto, que pode ser visualizado diretamente e com referência cruzada com as variáveis e restrições especificadas no modelo.
Introdução
Estrutura do AMPL:
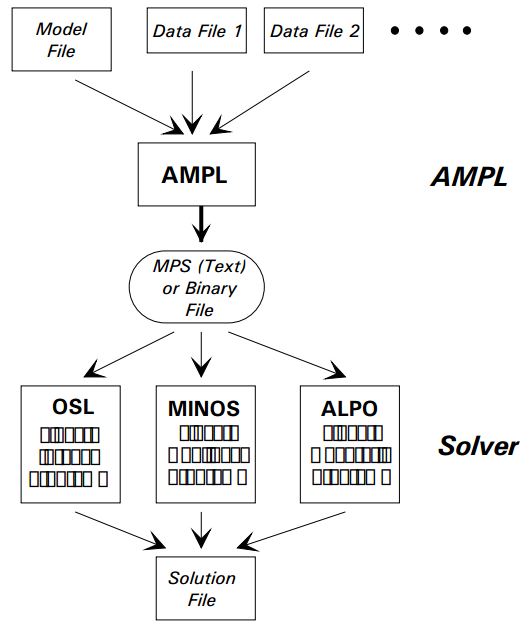
Alguns Solvers
CPLEX: O solver IBM ILOG CPLEX resolve problemas de programação inteiros, problemas de PL de grande porte usando variantes do método SIMPLEX ou o Método do Pontos Interiores, problemas de Progração Quadrática Convexa e Não-convexa e problemas Convexos com Restrições Quadráticas.
MINOS: MINOS é um solver para resolver problemas de otimização em larga escala (lineares e não-lineares). É especialmente eficaz para programas lineares e para problemas com função objetivo não-linear e restrições lineares.
Alguns Solvers
SNOPT: O SNOPT é usado para a solução de problemas de otimização de grande porte restritos não-linearmente. O SNOPT implementa um Algoritmo de Programação Sequencial que usa uma função Lagrangeana aumentada.
KNITRO: KNITRO é usado para resolver problemas de otimização não-convexos, restritos não-linearmente. Também pode ser usado para resolver problemas mais simples, como problemas sem restrições, problemas restritos limitados, problemas de PL e problemas de Programação Quadrática.
Introdução
Alguns solver e suas características:
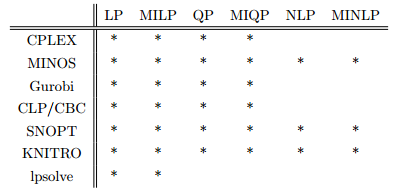
Versões Disponívels para Instalação
AMPL e alguns solvers são de uso comercial. Porém, geralmente é fornecida uma versão de estudante para cursos ou projetos de pesquisa relativamente simples.
Para instalar AMPL:
Versões Disponívels para Instalação
Para instalar AMPL:
Escolher a versão compatível para descarregar. Além disso, ao mesmo tempo, é recomendável descarregar uma versão de estudante dos solvers que trabalham com a AMPL.
Link útil http://ampl.com/try-ampl/download-a-demo-version/ $\rightarrow$ contém tanto o AMPL quanto solvers e exemplos.
Versões Disponívels para Instalação
Outra fonte é netlib (http://www.netlib.org/ampl/student/), que é um repositório de software matemático. As versões de tamanho limitado do AMPL e determinados solvers estão disponíveis gratuitamente para descarga a partir desta página. Essas versões não possuem requisitos de licenciamento ou data de validade. No entanto, são estritamente limitados ao tamanho do problema:
Para problemas lineares, 500 variáveis e 500 restrições mais objetivos.
Para problemas não-lineares, 300 variáveis e 300 restrições mais objetivos.
Sintaxe
Normalmente, um programa AMPL completo terá três partes:
Modelo (arquivo *.mod): Descrição do modelo matemático, que incluirá variáveis, parâmetros, função objetivo, restrições, etc.
Dados (arquivo *.dat): Conjunto específico de dados exatos utilizados no modelo, principalmente, é para parâmetros definidos no modelo.
Comando de execução (arquivo *.run): O comando Running é integrar os arquivos do modelo e dos dados através de comandos, além de definir as opções apropriadas do solver e do AMPL e exibir os resultados.
Declaração do Modelo
Na linha de comandos do AMPL, pode se iniciar a declaração do modelo da seguinte forma:
ampl: model; ampl: set N; ampl: param distance {i in N}; ampl: var x {i in N} >=0; ampl: s.t. c1 {i in N}: x[i] >= distance[i]; ... ampl: # ou simplesmente importar um arquivo .mod ampl: model dis.mod;
Declaração do Modelo - Conjuntos $\rightarrow$ set
No AMPL, set é uma palavra-chave usada para definir coleções finitas de elementos.
Esses elementos podem ser numéricos ou não-numéricos e, frequentemente, são usados como índices.
Alguns exemplos de declarações de conjuntos no arquivo de modelo (*.mod) e atribuições de valores (*.dat):
Arquivo *.mod Arquivo *.dat param n: set P := 1..n;param n:= 4;set Q;set Q := 1 2 3 4;set R;set R := rainy, cloudy, sunny;
Declaração do Modelo - Parâmetros $\rightarrow$ param
Normalmente, os parâmetros são importantes em um modelo matemático.
A maioria das análises do modelo são focadas em parâmetros.
No AMPL, usa-se param para declarar parâmetros, mantendo os valores declarados constantes.
Alguns exemplos de declarações de parâmetros (*.mod) e a correspondente atribuição de valores (*.dat):
Arquivo *.mod Arquivo *.dat param m1;param m1 := 1 1.2 2 1.5 3 1.4;param m2;param m2 := 1 1.2 2 1.5 3 1.4;
Declaração do Modelo - Parâmetros $\rightarrow$ param
Alguns exemplos de declarações de parâmetros (*.mod) e a correspondente atribuição de valores (*.dat):
Arquivo *.mod Arquivo *.dat set M; set O; param p{M,O};set M := a b c d; set O := e f g; param p: a b c d := e 1 5 3 2 f 4 3 1 0 g 3 2 7 8;param n: set M; set O; set N; param q{M,O,N};param n := 3; set M := a b c d; set O := e f g; set N := {1..n}; param q: [*,*,1]: a b c d := e 1 5 3 2 f 4 3 1 0 g 3 2 7 8;
Declaração do Modelo - Variáveis $\rightarrow$ var
No AMPL, usa-se var como palavra-chave para declarar variáveis.
Podem-se declarar variáveis em um arquivo *.mod (ou também em um arquivo *.run).
Alguns exemplos de declarações de variáveis no arquivo *.mod:
Arquivo *.mod var x;var x{N};var x{1..n} >= 0 <= 1;
Declaração do Modelo - Variáveis $\rightarrow$ var
Alguns exemplos de declarações de variáveis no arquivo *.mod:
var x{1..n,M} integer;var x{M,O,N} binary;Note-se que todas as declarações de variáveis estão em arquivos *.mod.
As restrições vinculadas às variáveis podem ser impostas na declaração das variáveis no arquivo *.mod. Por exemplo, impondo limites superiores e inferiores sobre o vetor das variáveis durante a declaração das variáveis.
As variáveis são assumidas como números reais. Se o problema exigir que uma variável ou vetor de variáveis seja restrito para ser inteiro ou binário, deve-se escrever o comando integer ou binary na frente da declaração da variável.
Declaração do Modelo - Maximizar/Minimizar $\rightarrow$ maximize/minimize
No AMPL, aplicam-se as palavras-chave maximize e minimize para definir a função objetivo.
Seguido de maximize ou minimize, deve-se definir o nome da função objetivo, como, por exemplo, custo, lucro, perdas etc. Após o nome da função objetivo, escreve-se a correspondente expressão da função objetivo.
Alguns exemplos:
Arquivo *.mod maximize profit: sum {i in Index} x[i]*profit[i];maximize cost: sum {i in Index} x[i]; maximize profit: sum {i in Index} x[i]*profit[i];
Declaração do Modelo - Maximizar/Minimizar $\rightarrow$ maximize/minimize
Alguns exemplos:
Arquivo *.mod maximize profit: sum {i in Index} x[i]*profit[i];maximize cost: sum {i in Index} x[i]; maximize profit: sum {i in Index} x[i]*profit[i];Conforme mostrado acima, pode-se usar sum {i in Index} para indicar uma soma de variáveis. Além disso, podem-se definir múltiplos objetivos.
Declaração do Modelo - Sujeito a $\rightarrow$ subject to
No AMPL, é usado subject to ou simplesmente s. t. para indicar uma restrição.
Como quando se define a função objetivo, também deve-se nomear cada restrição.
Alguns exemplos:
Arquivo *.mod subject to constA {i in 1..n}: x[i] <= b[i];subject to constB {i in N}: x[i,a] + x[i,b] <= c[i];
Declaração do Modelo - Sujeito a $\rightarrow$ subject to
Alguns exemplos:
Arquivo *.mod subject to constA {i in 1..n}: x[i] ≤ b[i];subject to constB {i in N}: x[i,a] + x[i,b] ≤ c[i];É bastante útil, pois não é necessário definir uma lista de restrições, definir um padrão especı́fico de restrições (geralmente no modelo, as restrições são do tipo $\small \forall i$).
Sugere-se que as variáveis tenham os limites superiores ou inferiores especificados na parte de declaração de variáveis (var), em vez de colocá-las na parte das restrições.
Definição dos Dados
Na linha de comando do AMPL, pode-se digitar, como mostrado a seguir, para atribuir dados para set (conjuntos) e param (parâmetros):
ampl: model dietu.mod; ampl: data; ampl data: set MINREQ := A B1 B2 C CAL; ampl data: set MAXREQ := A NA CAL; ...ou então importar do arquivo "dietu.dat":
ampl: # importar especificações de dados de um arquivo *.dat: ampl: data dietu.dat; ...
Definição dos Dados
Algumas vezes, precisa-se especificar um dado grande, por exemplo, uma sequência de tempo. Nesse caso, pode-se usar "{}" para indicar uma lista de valores:
ampl: set TIME := {1..100};o que significa uma sequência de tempo de 1 a 100, aumentando em 1 de cada vez.
Definição dos Dados
Algumas vezes também é necessário definir conjuntos ou parâmetros de duas dimensões.
AMPL possui um recurso para lidar com esse problema que consiste em especificar dados de duas dimensões como uma lista de pares.
ampl data: set LINKS := (GARY,DET) (GARY,LAN) (GARY,STL) (GARY,LAF) (CLEV,FRA) (CLEV,DET) (CLEV,LAN) (CLEV,WIN) (CLEV,STL) (CLEV,LAF) (PITT,FRA) (PITT,WIN) (PITT,STL) (PITT,FRE);Outra opção é especificar dados com ∗ tomando o lugar dos elementos que podem ser substituı́dos por outros. Esse tipo de recurso é muito mais útil em uma situação com dados de matrizes dispersas.
ampl data: set LINKS := (*,FRA) CLEV PITT (*,DET) GARY CLEV (*,LAN) GARY CLEV (*,WIN) CLEV PITT (*,LAF) GARY CLEV (*,FRE) PITT (*,STL) GARY CLEV PITT;
Solução do Problema - solve
AMPL usa MINOS como seu solver padrão; porém, se for necessário alterá-lo para CPLEX, por exemplo, pode-se digitar, na linha de comandos (ou no arquivo *.run), como segue:
ampl: model diet.mod; ampl: data diet.dat; ampl: option solver cplex ampl: solve; CPLEX 12.6.0.0: optimal solution: objective 88.2 1 dual simplex iterations (0 in phase I)Um solve diferente terá diferentes algoritmos para aplicar; asim, a saı́da pode ter algumas diferenças.
AMPL - Solução de um Problema Restrito - Exemplo 4.2.1
Resolver o seguinte problema usando AMPL:
$ \textrm{Min} \ f \left({ X }\right) = \left({ 1 - x_1 }\right)^2 + 100*\left({ x_2 - x_1^2 }\right)^2\\ \textrm{Sujeito} \ \textrm{a:} \\ \ \ \ \ x_1^2 + x_2^2 \leq 2 $
$ \textrm{Min} \ f \left({ X }\right) = \left({ 1 - x_1 }\right)^2 + 100*\left({ x_2 - x_1^2 }\right)^2\\ \textrm{Sujeito} \ \textrm{a:} \\ \ \ \ \ x_1^2 + x_2^2 \leq 2 $
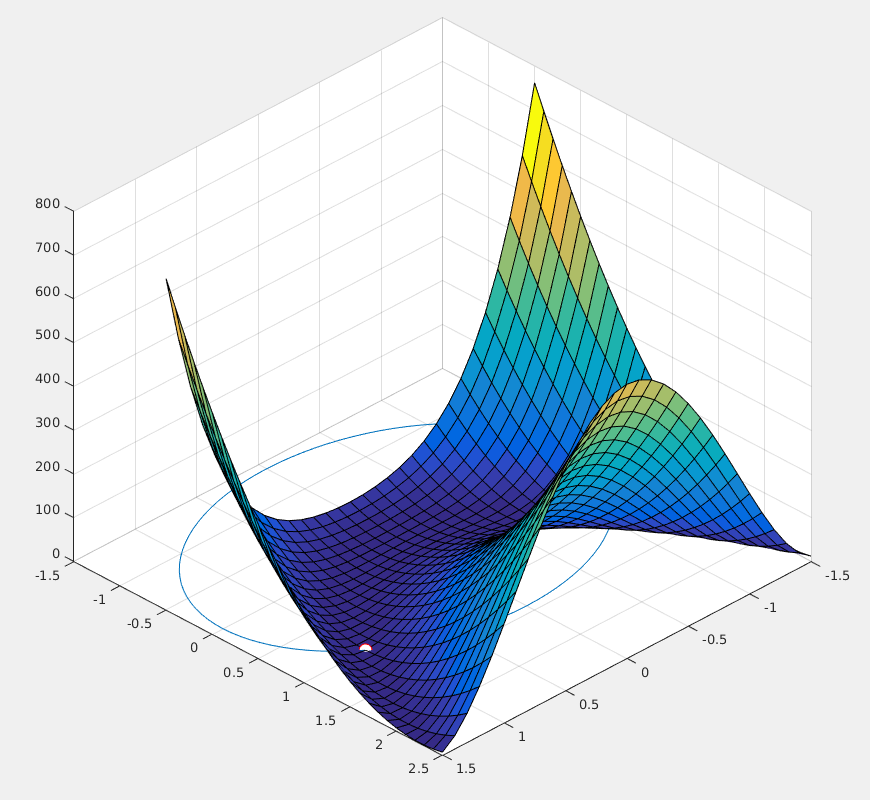
$ \textrm{Min} \ f \left({ X }\right) = \left({ 1 - x_1 }\right)^2 + 100*\left({ x_2 - x_1^2 }\right)^2\\ \textrm{Sujeito} \ \textrm{a:} \\ \ \ \ \ x_1^2 + x_2^2 \leq 2 $
Arquivo exemplo_restrito.mod:
# Variáveis:
var x1 >= -1.5, <= 1.5;
var x2 >= -0.5, <= 2.5;
# Função objetivo:
minimize z: (1 - x1)^2 + 100*(x2 - x1^2)^2;
# Restrições:
s.t. con1: x1^2 + x2^2 - 2 <= 0;
$ \textrm{Min} \ f \left({ X }\right) = \left({ 1 - x_1 }\right)^2 + 100*\left({ x_2 - x_1^2 }\right)^2\\ \textrm{Sujeito} \ \textrm{a:} \\ \ \ \ \ x_1^2 + x_2^2 \leq 2 $
Arquivo exemplo_restrito.dat:
# Valores iniciais:
let x1 := 0;
let x2 := 0;
$ \textrm{Min} \ f \left({ X }\right) = \left({ 1 - x_1 }\right)^2 + 100*\left({ x_2 - x_1^2 }\right)^2\\ \textrm{Sujeito} \ \textrm{a:} \\ \ \ \ \ x_1^2 + x_2^2 \leq 2 $
Arquivo exemplo_restrito.run:
reset;
model exemplo_PNL_restrito.mod;
data exemplo_PNL_restrito.dat;
option solver MINOS;
solve;
display _varname, _var;
display _objname, _obj;
display _conname, _con;
Resultados fornecidos pelo AMPL:
MINOS 5.51: optimal solution found.
41 iterations, objective 1.556515143e-17
: _varname _var :=
1 x1 1
2 x2 1
;
: _objname _obj :=
1 z 1.55652e-17
;
: _conname _con :=
1 con1 0
;
Otimização em Sistemas de Energia Elétrica
Departamento de Engenharia Elétrica