Otimização em Sistemas de Energia Elétrica

Universidade Federal do Espírito Santo

Departamento de Engenharia Elétrica

Prof. Augusto César Rueda Medina / CT-XI, Sala 27 / augusto.rueda@ufes.br
Logo Logo

Unidade 4

4.1. MATLAB

Introdução - Comandos e Estruturas de Controle

  • Toda linguagem de programação é constituı́da essencialmente por COMANDOS e ESTRUTURAS DE CONTROLE que o computador é capaz de interpretar e executar.

  • Os COMANDOS são ordens bastante primitivas como: ler um valor, imprimir um valor, somar dois valores, multiplicar dois valores, etc.

  • As ESTRUTURAS DE CONTROLE são uma espécie de comandos de nı́vel mais elevado, porque elas são utilizadas para gerenciar a execução dos comandos mais primitivos.

Introdução - Algoritmo

  • A sequência de comandos escritos para serem executados é chamada de ALGORITMO. Um algoritmo é um procedimento para solucionar determinado problema fazendo uso exclusivamente dos comandos e estruturas de controle que determinada linguagem de programação oferece.

  • Para resolver o mesmo problema podem se escrever inúmeros algoritmos diferentes. Assim, é possível resolver um problema específio como um algoritmo bem pequeno, ou com um algoritmo longo e, talvez, pouco funcional.

Comandos - Comando de leitura

  • Ao executar um Comando de Leitura aparece um pequeno cursor na tela, indicando que o computador está esperando que seja digitado um caracter no teclado. Após digitar o caracter, pressionando em seguida a tecla enter, o computador faz sua leitura e o armazena em uma posição na sua memória.

  • Comando input. Exemplo:

    
>> A = input(’Digite um valor para A’);

Comandos - Comando de impressão

  • Este comando é utilizado quando se deseja que o computador exiba na tela os valores que tem armazenado em diversas posições na memória.

  • Comando disp. Exemplos:

    
>> disp(A);                         % Exibe o valor da variável A
>> disp('Exibe este texto');        % Exibe uma mensagem

Comandos - Comando de atribuição

  • O Comando de Atribuição é também chamado de Comando Aritmético porque é nele que são definidas as expressões aritméticas necessárias para a resolução de um problema qualquer. Ao executar um comando de atribuição, o computador armazena, na variável cujo nome é mencionado à esquerda do sinal de igual (=) o valor da expressão aritmética especificada à direita deste sinal.

  • Exemplos:

    
>> a = 5                    % Atribui o valor 5 a variável a
>> b = a + 10               % Atribui à variável b o valor de a mais 10
>> b = b + 1                % Atribui à variável b o valor de b mais 1
>> c = ’Hello world’        % Atribui à variável c a mensagem Hello world

Estrutura de decisão

  • Esta estrutura força o computador a tomar uma decisão quanto à executar ou não e uma determinada sequência de comandos. Existem duas estruturas distintas: a estrutura if de um único ramo, ou uma única alternativa; e a estrutura if (else) de dois ramos, ou duas alternativas.

  • Estrutura if de um único ramo:

    
if <COMPARAÇÃO>
    % Comandos e outras estruturas;
end

  • Pode-se entender a estrutura if da seguinte forma: Se <COMPARAÇÃO> for verdadeira, então Comandos e outras estruturas são executados; caso contrário, ou seja, se <COMPARAÇÃO> for falso, então o computador dá um "salto" para logo após o end.

Estrutura de decisão

  • Estrutura if de dois ramo:

    
if <COMPARAÇÃO>
    % Comandos e outras estruturas 1;
else
    % Comandos e outras estruturas 2;
end

  • Nessa estrutura, se a <COMPARAÇÃO> for verdadeira, então Comandos e outras estruturas 1 são executados e Comandos e outras estruturas 2 não são executados; caso <COMPARAÇÃO> for falso, então Comandos e outras estruturas 2 são executados e Comandos e outras estruturas 1 não são executados.

Estrutura de decisão

  • Exemplo:

    
A = input(’Digite um valor para A’);                         % Armazena um valor em A
B = input(’Digite um valor para B’);                         % Armazena um valor em B

if A < B                                                    % Compara A e B
    disp(’A variável A é menor que a variável B’);           % Executa disp (Comando 1)
else
    disp(’A variável A é maior ou igual que a variável B’);  % Executa disp (Comando 2)
end

Estrutura de repetição for

  • Estrutura for: Esta estrutura serve para repetir uma determinada quantidade de vezes a execução de um ou mais comandos. O formato geral da estrutura de repetição for é dado por:

    
for i=j:k:M
    % Comandos e outras estruturas
end

  • A variável i começa valendo j, e, adicionando-se um valor k, ela cresce (ou decresce) até M. Em cada acréscimo da variável i, Comandos e outras estruturas é executado. Caso k = 1 ao final teremos M - j + 1 repetições de Comandos e outras estruturas:

Estrutura de repetição for

  • Exemplo: No programa a seguir, a palavra Mundo é repetida 3 vezes:

    
for i=3:1:5
    disp(’Mundo’);
end

Estrutura de repetição while

  • O while é uma estrutura de repetição que funciona similar à estrutura for. while e for são estruturas de repetição que diferem entre si na forma como é definida execução dos ciclos. Ambas foram projetadas para fazer o computador repetir uma determinada quantidade de vezes a execução de um bloco de comandos. O formato geral da estrutura de repetição while é dado por:

    
while <COMPARAÇÃO>
    % Comandos e outras estruturas
end

  • Enquanto a <COMPARAÇÃO> for verdadeira Comandos e outras estruturas é executado. O fim da repetição acontece quando <COMPARAÇÃO> se torna falsa.

Estrutura de repetição while

  • Exemplo: No programa a seguir, a palavra Mundo é repetida 5 vezes:

    
A=5;                    % Armazena o valor 5 em A
while A < 10
    disp(’mundo’);
    A=A+1;
end

Itens Básicos do MATLAB

  • Operadores relacionais:

    <
    		 Menor que 
    <=
    		 Menor ou igual que 
    >
    		 Maior que 
    >=
    		 Maior ou igual que 
    =
    		 Igual a 
    ~=
    		 Diferente de

Itens Básicos do MATLAB

  • Conectivos lógicos:

    &
    		 E 
    |
    		 Ou 
    ~
    		 Não 
    Xor
    		 Ou excludente

Itens Básicos do MATLAB

  • Funções pré-definidas:

    cos(x)
    		 Retorna ao cosseno de $x$ 
    sin(x)
    		 Retorna ao seno de $x$ 
    ∧
    		 Potência. Exemplo: $5^2$: 
    5∧2 = 25
    		 
    exp(x)
    		 Retorna a $e^x$ 
    log(x)
    		 Retorna ao $ln(x)$ 
    sqrt(x)
    		 Retorna a $\sqrt x $

Itens Básicos do MATLAB

  • Funções pré-definidas (continuação):

    abs(x)
    		 Valor absoluto de $x$ ou $|x|$ 
    isreal(x)
    		 Verdadeiro para valores reais de $x$ 
    fix(x)
    		 Arredondamento na direção do zero 
    floor(x)
    		 Arredondamento na direção de $-\infty$ 
    ceil(x)
    		 Arredondamento na direção de $+\infty$ 
    round(x)
    		 Arredondamento para o inteiro mais próximo

Itens Básicos do MATLAB

  • Funções pré-definidas (continuação):

    det(A)
    		 Determinante da matriz A 
    inv(A)
    		 Inversa da matriz A 
    size(A)
    		 Retorna a dimensão da matriz A 
    cross(v, w)
    		 Produto vetorial $v \times w$ 
    sum(v. ∗ w)
    		 Produto interno <$v$,$w$>

Scripts

  • A janela de comandos do MATLAB não é suficiente para escrever programas extensos. Por isso, é necessário criar um script (programa). Um script nada mais é do que uma lista de comandos e estruturas que são executados sequencialmente. Para criar um script, basta clicar em Arquivo >> Novo.

  • Exemplo: Criar um script para somar o primeiros 100 números.

    
soma=0;

for i=1:1:100
    soma = soma + i;
end

disp(soma);

Scripts

  • Exemplo: Script para encontrar e imprimir o menor valor de 3 números.

    
a = input(’digite o primeiro número’);
b = input(’digite o segundo número’);
c = input(’digite o terceiro número’);

if a < b
    if a < c
        disp(a);
        disp(’ é o menor valor’);
    else
        disp(c);
        disp(’ é o menor valor’);
    end
else
    if b < c
        disp(b);
        disp(’ é o menor valor’);
    else
        disp(c);
        disp(’ é o menor valor’);
    end
end

Scripts

  • Exemplo: Script para ler um número inteiro positivo $N$ e calcular $S$, onde:

    \[ \scriptsize S = \frac{1}{1} + \frac{3}{2} + \frac{5}{3} + \frac{7}{4} + \cdots + \frac{I}{N}\]

    
N = input(’digite o número inteiro positivo N’);

S = 0;
I = 1;

for j=1:1:N
    S = S + (I/j);
    I = I + 2;
end

disp(’O valor de S é: ’);
disp(S);

Vetores e Matrizes

  • Um vetor pode ser considerado como uma variável múltipla, ou seja, uma variável que possui outras variáveis. Assim o vetor $V = \left[ {\begin{array}{*{20}{c}} 1 & 0 & 0 & 5 & 6 \end{array}} \right]$, por exemplo, é considerado um vetor de 5 posições. Cada elemento do vetor $V$ pode ser obtido por referência à posição. Assim $V(1) \ = \ 1$, $V(2) \ = \ 0$, $V(3) \ = \ 0$, $V(4) \ = \ 5$ e $V(5) \ = \ 6$.

  • O mesmo vale para matrizes. Se por exemplo,

    \[ \scriptsize M = \left[ {\begin{array}{*{20}{c}} 1 & 3 & 0\\ 3 & 3 & 3\\ 2 & 1 & 8 \end{array}} \right]\]

    Podemos fazer referência aos elementos de $M$ da seguinte forma: $V(i,j)$ onde $i$ é a linha e $j$ a coluna.

Vetores e Matrizes

  • Exemplos:

    
>> V = [1 1 0]
V =
    1   1   0
    
>> 5*V
ans =
    5   5   0
    
>> K = [2 3 5]
K =
    2   3   5
    
>> V + K
ans =
    3   4   5
    
>> M = [1 3 0; 3 3 3; 2 1 8]
M =
    1   3   3
    3   3   3
    2   1   8

>> M(1,3)
ans = 0

>> M(2,3)
ans = 3

>> M(2,2)
ans = 3

>> c = 7*M(2,2)
c = 21

>> 2*M
ans =
    2   6   0
    6   6   6
    4   2   16

Funções

  • Uma função em MATALB é bem parecida com uma função matemática, ou seja, dado um valor $x$ a função se associa a um valor $y$. O valor $x$ é chamado de entrada e $y$ de saı́da.

  • Assim a função $f\left( x \right) = x^2$ pode ser construı́da da seguinte forma:

    
function [f_val] = f (x)

    f_val = x^2;
    
end

Funções

  • Quando retornamos para a linha de comando (<<) basta aplicar a função $f\left( x \right)$ em um número qualquer que teremos o quadrado desse número. Por exemplo:

    
>> f(2)
    ans = 4
    
>> f(3)
    ans = 9

  • Nota: Cada função deve ser salva com o mesmo nome do cabeçalho.

Gráficos Bidimensionais

  • O processo para criar um gráfico de uma função $f\left( x \right)$ é relativamente simples. Cria-se uma tabela de pontos com valores $\left( x,y \right)$ e marca-se estes pontos no plano cartesiano. Por exemplo, o passo a passo a construção do gráfico da função $f\left( x \right) = x^2$, no intervalo $[−3 \ \ 3]$, é dado da seguinte forma:

    • Passo 1: Cria-se a função $f\left( x \right) = x^2$.

    • Passo 2: Cria-se o vetor $x$ com espaçamento de $1/100 = 0.01$ no intervalo $[−3 \ \ 3]$.

      
x = −3:0.01:3;

    • Passo 3: Como não é conhecido o tamanho do vetor $x$, então é usada a função pré-definida size() para descobrir o tamanho do vetor $x$ e, assim, calcular o vetor $y = f\left( x \right)$.

      
[L,C] = size(x);

for i=1:C
    y = f(x(i));
end

Gráficos Bidimensionais

  • Passo a passo a construção do gráfico da função $f\left( x \right) = x^2$, no intervalo $[−3 \ 3]$ (continuação):

    • Passo 4: Para traçar o gráfico, basta usar a função pré-definida plot(). Essa função marca, no plano cartesioano, os pontos $\left( {{x_i},{y_i}} \right)$ dos vetores $x$ e $y$.

      
plot(x,y);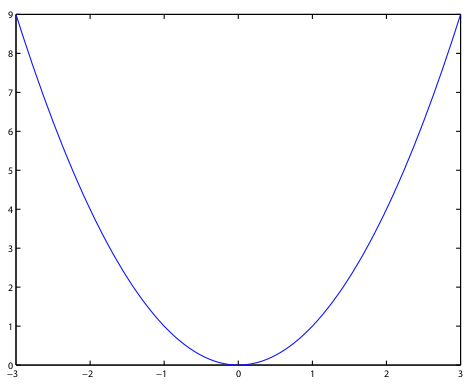

Gráficos Bidimensionais

  • Modo rápido: O modo com que criamos o gráfico anterior, permite mais controle sobre o mesmo. Mas existe uma outra forma de construir mais rapidamente o gráfico de $f\left( x \right)$. Veja:

    
>> x = −3:0.01:3;

>> y = x.^2;

>> plot(x, y);

Gráficos Tridimensionais

  • O processo para construir gráficos tridimensionais é parecido com o de construção de gráficos bidimensionais. Por exemplo, na construção do gráfico de $f\left( x, y \right) = x_2 + y_2$ nos intervalos definido pelo espaço $D = [−1 \ \ 1] \times [−2 \ \ 3]$.

    
>> [X,Y] = meshgrid(−1:0.1:1,−2:0.1:3);

>> Z = X.^2 + Y.^2;      % Z é uma matriz, por isso, usamos X. e Y. no cálculo.

Gráficos Tridimensionais

  • Para traçar o gráfico pode ser usada a função pré-definida surf(Z).

    
>> surf(Z);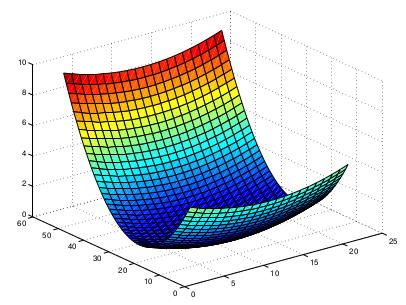

Gráficos Tridimensionais

  • As curvas de nı́vel podem ser construı́das com a função pré-definida contour(Z).

    
>> contour(Z);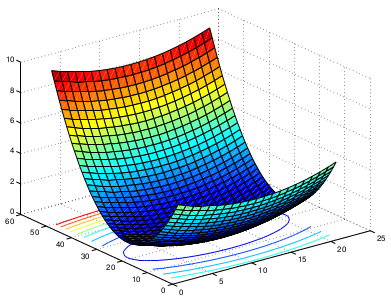

Otimização em Sistemas de Energia Elétrica

Universidade Federal do Espírito Santo

Departamento de Engenharia Elétrica

Prof. Augusto César Rueda Medina / CT-XI, Sala 27 / augusto.rueda@ufes.br
Logo Logo