Análise de Sistemas de Energia Elétrica

Universidade Federal do Espírito Santo

Departamento de Engenharia Elétrica

Prof. Augusto César Rueda Medina / CT-XI, Sala 27 / augusto.rueda@ufes.br

Unidade 8

Estudos de Estabilidade

8.4. Análise de Estabilidade Angular de Grandes Perturbações

Estudos de Estabilidade - Sistema Máquina Barramento Infinito

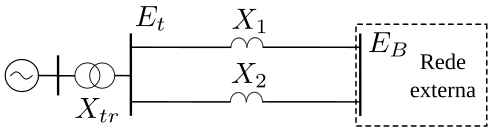
Considere-se o seguinte gerador ligado a uma linha que, por sua vez, está conectada à rede externa:

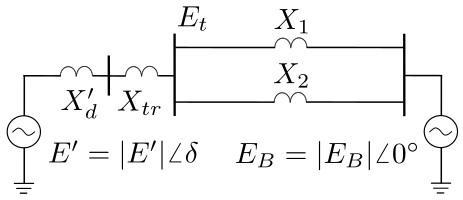
Incluindo o circuito equivalente do gerador síncrono:

Estudos de Estabilidade - Sistema Máquina Barramento Infinito

Simplificando:

$\small {X}_{{T}} = {{X'}}_{{d}} + {\rm{X}}_{\rm{E}} $

Estudos de Estabilidade - Sistema Máquina Barramento Infinito

$\small {I}_{{t}} = \frac{{{E'}} - {{E}}_{{B}} \angle{-\delta}}{j{{X}}_{{T}}} = \frac{{{E'}} - {{E}}_{{B}} \left( { cos \left(-\delta \right) - j sen \left( -\delta \right) } \right) }{j{{X}}_{{T}}} $

$\small {I}_{{t}} = \frac{{{E'}} - {{E}}_{{B}} \left( { cos \left(-\delta \right) - j sen \left( -\delta \right) } \right) }{j{{X}}_{{T}}} $

$\small {S'}_{{t}} = {E'} {I}^{*}_{{t}} $

$\small {S'}_{{t}} = {E'} \left( \frac{{{E'}} - {{E}}_{{B}} \left( { cos \left(-\delta \right) - j sen \left( -\delta \right) } \right) }{j{{X}}_{{T}}} \right)^{*} $

Estudos de Estabilidade - Sistema Máquina Barramento Infinito

$\small {S'}_{{t}} = {E'} \left( \frac{{{E'}} - {{E}}_{{B}} \left( { cos \left(-\delta \right) - j sen \left( -\delta \right) } \right) }{j{{X}}_{{T}}} \right)^{*} $

$\small {S'}_{{t}} = \frac{{{E'}} {{E}}_{{B}} sen \delta }{{{X}}_{{T}}} + j \frac{ {{E'}} \left( {{E'}} - {{E}}_{{B}} cos \delta \right) }{{{X}}_{{T}}} $

$\small { {P}}_{ {e}} = {{\rm Re}} \left\{ { {S'}_{{t}} } \right\} $

$\small { {P}}_{ {e}} = \frac{{{E'}} {{E}}_{{B}} sen \delta }{{{X}}_{{T}}} $

Potência máxima fornecida pelo gerador:

$\small \boxed{ { {P}}_{ {e,max}} = \frac{{{E'}} {{E}}_{{B}} }{{{X}}_{{T}}} }$

Estudos de Estabilidade - Sistema Máquina Barramento Infinito

Representação gráfica:

Estudos de Estabilidade - Mudança na Potência Mecânica

Resposta à mudança na potência mecânica:

Estudos de Estabilidade - Mudança na Potência Mecânica

Equações de Movimento ou Swing:

$\small p \left( { \Delta \omega_{ {r}} } \right) = \frac{ 1 }{2 { {\rm {H}}}} \left( { { {T}}_{ {m}} - { {T}}_{ {e}} - {\rm {K}}_{\rm {D}} \Delta \omega_{ {r}} } \right) $

$\small p \left( { \delta } \right) = \omega_{ {0}} \Delta \omega_{ {r}} $

sendo:

$\small p$: Operador diferencial $\small p=d/dt$.
$\small \Delta \omega_{ {r}}$: Variação da velocidade.
$\small \omega_{ {0}}$: Velocidade do rotor.
$\small T_{\rm {m}}$: Torque mecânico no rotor.
$\small {\rm {K}}_{\rm {D}}$ e ${\rm {H}}$: Coeficiente de torque de amortecimento e costante de inércia.

Estudos de Estabilidade - Critêrio das Áreas Iguais

$\small p \left( { \Delta \omega_{ {r}} } \right) = \frac{ 1 }{2 { {H}}} \left( { { {T}}_{ {m}} - { {T}}_{ {e}} - { {K}}_{ {D}} \Delta \omega_{ {r}} } \right) $

$\small p \left( { \delta } \right) = \omega_{ {0}} \Delta \omega_{ {r}} $

Substituindo a segunda equação de movimento na primeira:

$\small 2 p^2 \left( { \delta } \right) = \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) $

Aplicado $\small p \ \delta$ em ambos lados da equação:

$\small \boxed{ p \ \delta } \ 2 p^2 \left( { \delta } \right) = \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) \ \boxed{ p \ \delta } $

$\small 2 p \left( { p \ \delta } \right)^2 = \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) p \ \delta $

Integrando em ambos lados:

$\small \left( { \frac{ d \ \delta}{d \ { {t}}} } \right)^2 = \int { \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) d \ \delta } $

Estudos de Estabilidade - Critêrio das Áreas Iguais

$\small \left( { \frac{ d \ \delta}{d \ { {t}}} } \right)^2 = \int { \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) d \ \delta } $

Para que exista estabilidade, a área total entre os limites $\small \delta_0$ e $\small \delta_{max}$ deve ser zero. Assim, tem-se que:

$\small \boxed { \int^{\delta_{ {max}}}_{\delta_{ {0}}} { \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) d \ \delta } = 0 } $

Estudos de Estabilidade - Critêrio das Áreas Iguais

$\small \boxed { \int^{\delta_{ {max}}}_{\delta_{ {0}}} { \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) d \ \delta } = 0 } $

Considere-se a máquina operando no ponto de equilíbrio $\small \delta_0$, correspondente à potência mecânica $\small P_{m,0} = P_{e,0}$.

Considere-se agora um súbito incremento na entrada de potência, representada por $\small P_{m,1}$.

Como $\small P_{m,1} > P_{e,0}$, a potência acelerante no rotor é positiva e o ângulo $\small \delta$ aumenta.

A energia armazenada no rotor durante esta aceleração é $\small A_1$.

Estudos de Estabilidade - Critêrio das Áreas Iguais

$\small \boxed { \int^{\delta_{ {max}}}_{\delta_{ {0}}} { \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) d \ \delta } = 0 } $

Com o aumento em $\small \delta$, a potência elétrica também aumenta, e, quando $\small \delta = \delta_{1}$, a potência elétrica alcança seu novo ponto $\small P_{m,1}$. Embora a potência acelerante neste ponto seja zero, o rotor está girando acima da velocidade síncrona, já que $\small \delta$ e $\small P_{e}$ continuaram a aumentar.

Agora $\small P_{m,1} < P_{e}$, o que causa que o rotor desacelere em direção à velocidade síncrona até que $\small \delta = \delta_{max}$.

Estudos de Estabilidade - Critêrio das Áreas Iguais

$\small \boxed { \int^{\delta_{ {max}}}_{\delta_{ {0}}} { \frac{ \omega_{ {0}} }{{ {H}}} \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) d \ \delta } = 0 } $

A energia cedida pelo rotor quando desacelera em direção à velocidade síncrona é $\small A_2$.

O resultado é que o rotor oscila em torno da velocidade correspondente ao ângulo $\small \delta_1$ fazendo com que $\small A_1 = A_2$.

O amortecimento da máquina fará com que o rotor oscile entre $\small \delta_0$ e $\small \delta_{max}$ até se estabilizar no novo ponto de equilíbrio $\small \delta_1$.

Estudos de Estabilidade - Critêrio das Áreas Iguais

Definição das áreas $\small A_1$ e $\small A_2$:

$\small \boxed { { {A}}_1 = \int^{\delta_{ {1}}}_{\delta_{ {0}}} { \left( { { {P}}_{ {m}} - { {P}}_{ {e}} } \right) d \ \delta } } \ \ \ \ \ \ \boxed { { {A}}_2 = \int^{\delta_{ {max}}}_{\delta_{ {1}}} { \left( { { {P}}_{ {e}} - { {P}}_{ {m}} } \right) d \ \delta } } $

Estudos de Estabilidade - Critêrio das Áreas Iguais

Assim, o gerador permanecerá ESTÁVEL se $\small \boxed { { {A}}_1 \leq { {A}}_2} $

Estudos de Estabilidade - Resposta à Falta de uma Linha

Assumindo um curto-circuito na linha 2 do seguinte sistema:

O sistema de proteção isolará a linha em curto:

Estudos de Estabilidade - Resposta à Falta de uma Linha

Caso 1: O sistema volta à estabilidade.

Estudos de Estabilidade - Resposta à Falta de uma Linha

Caso 2: O sistema não volta à estabilidade.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Assuma-se agora um curto-circuito trifásico temporário no extremo emissor da linha 2:

Quando o curto-circuito é no extremo emissor da linha, não há potência transmitida ao barramento infinito. Como a resistência da linha está sendo desconsiderada, então a potência elétrica $\small P_e$ é zero.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Como $\small P_e$ é zero, então a curva corresponde ao eixo horizontal.

A máquina acelera com potência de entrada total como potência acelerante, aumentando assim sua velocidade, armazenando energia e aumentando seu ângulo $\small \delta$.

Quando a falta é esclarecida, é assumido que ambas linhas permanecem intactas.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

A falta é esclarecida em $\small \delta_1$ o que muda a operação da máquina ao ponto correspondente a $\small e$.

Nesse instante, a potência da rede está desacelerando e a energia, previamente armazenada, é reduzida a zero no ponto $\small f$, quando a área $\small A_2$ iguala a área $\small A_1$.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Como $\small P_e$ é ainda maior que $\small P_m$, o rotor continua a desacelerar e o ângulo $\small \delta$ pasa de novo pelo ponto $\small e$.

O ângulo do rotor então oscila voltando ao valor original de $\small \delta_0$, na sua frequência natural.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

O ângulo crítico é alcançado quando qualquer incremento adicional em $\small \delta_1$ causa que a área $\small A_2$ (energia desacelerante) seja menor que a área $\small A_1$ (energia acelerante).

Isto acontece quando $\small \delta_{max}$, ou ponto $\small f$, está na interseção entre a linha $\small P_m$ e a curva, como mostrado na figura anterior.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Aplicando o critério das áreas iguais (com $\small P_e = 0$) para determinar o ângulo crítico, tem-se que:

$\small { { {A}}_1 = \int^{\delta_{ {c}}}_{\delta_{ {0}}} { { {P}}_{ {m}} \ d \ \delta } } ={ { {A}}_2 = \int^{\delta_{ {max}}}_{\delta_{ {c}}} { \left( { P_{max} sen \delta - { {P}}_{ {m}} } \right) d \ \delta } } $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Integrando ambos lados, tem-se que:

$\small P_m (\delta_c - \delta_0) = P_{max} (cos \delta_c - cos \delta_{max} ) - P_m ( \delta_{max} - \delta_c ) $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

$\small P_m (\delta_c - \delta_0) = P_{max} (cos \delta_c - cos \delta_{max} ) - P_m ( \delta_{max} - \delta_c ) $

Resolvendo para $\delta_c$, tem-se que:

$\small \boxed{ cos \delta_c = \frac{P_{m}}{P_{max}} ( \delta_{max} - \delta_0 ) + cos \delta_{max} }$

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

A aplicação do critério das áreas iguais faz possível determinar o ângulo $\delta_c$ no qual a máquina permanece estável; porém, o correspondente tempo crítico deve ser determinado resolvendo o sistema de equações não lineares (equações de movimento).

Para este caso particular, em que a potência elétrica durante a falta é zero ($\small P_e = 0$), pode ser obtida uma solução analítica para determinar o tempo crítico $\small t_c$.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Das equações de movimento, e com $\small P_e = 0$, tem-se que:

$\small \frac{H}{\pi f_0} p^2 \left( { \delta } \right) = {P}_{ {m}} $

ou:

$\small \frac{H}{\pi f_0} \frac{ d^2 \delta}{d t^2} = {P}_{ {m}} $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

$\small \frac{H}{\pi f_0} \frac{ d^2 \delta}{d t^2} = {P}_{ {m}} $

Integrando ambos lados, tem-se que:

$\small \frac{d \delta}{d t} = \frac{ \pi f_0}{H} {P}_{ {m}} \int^{0}_{t} {d t} = \frac{ \pi f_0}{H} {P}_{ {m}} t $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

$\small \frac{d \delta}{d t} = \frac{ \pi f_0}{H} {P}_{ {m}} \int^{0}_{t} {d t} = \frac{ \pi f_0}{H} {P}_{ {m}} t $

Integrando, de novo, tem-se que:

$\small \delta = \frac{ \pi f_0}{2 H} {P}_{ {m}} t^2 + \delta_0 $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

$\small \delta = \frac{ \pi f_0}{2 H} {P}_{ {m}} t^2 + \delta_0 $

Assim, se o ângulo crítico é $\small \delta_c$, então o correspondente tempo crítico, $t_c$, é:

$\small \boxed{ t_c = \sqrt{ \frac{2 H (\delta_c - \delta_0)}{\pi f_0 P_m} } } $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Assuma-se agora que o curto-circuito trifásico temporário se apresenta, de novo na linha 2, mas a igual distância dos dois extremos da linha:

Quando o curto-circuito é nesse ponto da da linha, a reatância equivalente entre as barras diminui a capacidade de transferência de potência.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Quando a falta trifásica ocorre, o ponto de operação da máquina muda imediatamente para o ponto $\small b$ da curva $\small B$.

O excesso da potência mecânica de entrada sobre a potência elétrica de saída, acelera o rotor, armazenando-se energia, e o ângulo $\small \delta$ aumenta.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Assumindo que a falta é removida em $\small \delta_1$ isolando a linha em falta (linha 2), o ponto de operação da máquina então muda para $\small e$, na curva $\small C$.

A potência da rede está nesse momento desacelerando e a energia, previamente armazenada, é reduzida a zero no ponto $\small f$, quando a área $\small A_2$ igual a área $\small A_1$.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Como $\small P_e$ é ainda maior que $\small P_m$, então o rotor continua desacelerando passando, de novo, pelo ponto $\small e$.

O ângulo do rotor oscilará então em torno do ponto $\small e$ até alcançar um novo ponto de operação estabelecido pela interseção de $\small P_m$ e a curva $\small C$ (em $\small \delta_1$).

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

O ângulo crítico é alcançado quando qualquer incremento adicional de $\delta_1$ causa que a área $\small A_2$ (energia desacelerante) seja menor que a área $\small A_1$ (área acelerante).

Isto acontece quando $\small \delta_{max}$ , ou ponto $\small f$, está na interseção da linha $\small P_m$ com a curva $\small C$.

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Aplicando o critério das áreas iguais para determinar o ângulo crítico, tem-se que:

$\small { {P}}_{ {m}} ( \delta_c - \delta_0 ) - \int^{\delta_{ {c}}}_{\delta_{ {0}}} { { {P}}_{ {2,max}} sen \delta \ d \ \delta } = \int^{\delta_{ {max}}}_{\delta_{ {c}}} { P_{3,max} sen \delta \ d \ \delta } - { {P}}_{ {m}} (\delta_{max} - \delta_c) $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Integrando ambos lados e resolvenco para $\small \delta_c$, tem-se que:

$\small \boxed{ cos \delta_c = \frac{ { {P}}_{ {m}} ( \delta_{max} - \delta_0 ) + P_{3,max} cos \delta_{max} - P_{2,max} cos \delta_{0} }{ P_{3,max} - P_{2,max} } } $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Resumo - aplicação de um curto-circuito trifásico no extremo emissor:

$\small { cos \delta_c = \frac{P_{m}}{P_{max}} ( \delta_{max} - \delta_0 ) +\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ cos \delta_{max} }$

$\small { t_c = \sqrt{ \frac{2 H (\delta_c - \delta_0)}{\pi f_0 P_m} } } $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico

Resumo - aplicação de um curto-circuito trifásico no meio da linha:

$\small { cos \delta_c = \\ \ \ \frac{ { {P}}_{ {m}} ( \delta_{max} - \delta_0 ) + P_{3,max} cos \delta_{max} - P_{2,max} cos \delta_{0} }{ P_{3,max} - P_{2,max} } } $

Estudos de Estabilidade - Aplicação de um Curto-Circuito Trifásico - Exemplo 8.4.1

Um gerador de indução de 60 Hz com constante de inércia $\small H =$ 5 MJ/MVA está conectado a um barramento infinito através de um circuito puramente reativo, como mostrado na figura a seguir:

O gerador está fornecendo potência ativa $\small P_e = 0,8$ pu e potência reativa $\small Q = 0,074$ pu ao barramento infinito a uma tensão $\small V =$ 1 pu.

O fluxo de corrente no barramento infinito é:

$\small I = \frac{S^*}{V^*} = \frac{0,8 - j0,074}{1,0 \angle 0^{\circ}} = 0,8 - j0,074$ pu

A reatância de transferência entre a tensão interna do gerador e o barramento infinito antes da falta é:

$\small X_1 = 0,3 + 0,2 + \frac{0,3}{2} = 0,65$ pu

A tensão interna transitória é:

$\small E' = V + j X_1 I = 1,0 + j 0,65 ( 0,8 - j 0,074 ) = 1,17 \angle 26,387^{\circ} $ pu

(a) Uma falta temporária ocorre no extremo emissor da linha, no ponto $\small F$. Quando a falta é retirada, ambas linhas permanecem intactas. Determinar o ângulo e tempo críticos.

Como as duas linhas permanecem intactas quado a falta é retirada, então a equação do ângulo do rotor é:

$\small P_{max} sen \delta = \frac{ |E'| |V| }{ X_1 } sen \delta = \frac{(1,17)(1,0)}{0,65} sen \delta = 1,8 sen \delta $

O ângulo de operação inicial então é dado por:

$\small 1,8 sen \delta_0 = P_e = 0,8 $

ou:

$\small \delta_0 = 26,388^{\circ} = 0,46055$ rad

Usando a figura acima para determinar $\delta_{max}$, tem-se que:

$\small \delta_{max} = 180^{\circ} - \delta_0 = 153,612^{\circ} = 2,681$ rad

Como a falta é no começo da linha de transmissão, então a potência transferida durante a falta é zero e o ângulo crítico é dado por:

$\small cos \delta_c = \frac{P_m}{P_{max}} (\delta_{max} - \delta_0) + cos \delta_{max} \\ \ \ \ = \frac{0,8}{1,8} (2,681 - 0,46055) + cos 153,61^{\circ} = 0,09106$

Assim, o ângulo crítico é:

$\small \delta_c = cos^{-1} (0,09106) = 84,775^{\circ} = 1,48$ rad

O tempo crítico é dado por:

$\small t_c = \sqrt{\frac{ 2 H (\delta_c - \delta_0) }{ \pi f_0 P_m }} = \sqrt{\frac{ (2) (5) (1,48 - 0,46055) }{ \pi (60)(0,8) }} = 0,26 \ {\rm {s}} $

(b) Uma falta ocorre no meio da linha, no ponto $\small F$. Quando a falta é retirada, a linha em falta é isolada. Determinar o ângulo crítico.

A curva de potência, antes da falta, é igual à curva do caso anterior. Assim:

$\small P_{1,max} = 1,8 sen \delta$

De maneira similar, o gerador está operando ao ângulo inicial $\small \delta_0 = 26,388^{\circ} = 0,46055$ rad.

A falta ocorre no ponto $\small F$, no meio de uma linha, resultando no circuito mostrado na figura a seguir:

A reatância de transferência durante a falta, pode ser determinada de forma mais precisa convertendo o circuito $\small Y$ ABCF em seu equivalente $\small \Delta$, eliminando o ponto $\small C$. Assim, o circuito resultante é:

$\small X_{2} = \frac{ (0,5) (0,3) + (0,5) (0,15) + (0,3) + (0,15) }{ 0,15 } = 1,8$ pu

A curva da potência elétrica, durante a falta, é definida por:

$\small P_{2,max} sen \delta = \frac{ (1,17) (1,0) }{ 1,8 } sen \delta = 0,65 sen \delta$

Quando a falta é retirada, a linha em falta é isolada. Portanto, a reatância de transferência pós-falta é:

$\small X_{3} = 0,3 + 0,2 + 0,3 = 0,8$ pu

e a curva da potência elétrica é definida por:

$\small P_{3,max} sen \delta = \frac{ (1,17) (1,0) }{ 0,8 } sen \delta = 1,4625 sen \delta$

Usando a figura acima para determinar $\delta_{max}$, tem-se que:

$\small \delta_{max} = 180^{\circ} - sen^{-1} \left( { \frac{ 0,8 }{ 1,4625 } } \right) = 146,838^{\circ} = 2,5628$ rad

Aplicando a expressão para o cálculo do ângulo crítico, tem-se que:

$\small cos \delta_c = \frac{ { {P}}_{ {m}} ( \delta_{max} - \delta_0 ) + P_{3,max} cos \delta_{max} - P_{2,max} cos \delta_{0} }{ P_{3,max} - P_{2,max} } \\ \ \ \ = \frac{0,8 (2,5628 - 0,46055) + 1,4625 cos 146,838^{\circ} - 0,65 cos 26,388^{\circ} }{1,4625 - 0,65} = -0,15356$

Assim, o ângulo crítico é:

$\small \delta_{c} = cos^{-1} (-0,15356) = 98,834^{\circ}$ rad

Análise de Sistemas de Energia Elétrica

Universidade Federal do Espírito Santo

Departamento de Engenharia Elétrica

Prof. Augusto César Rueda Medina / CT-XI, Sala 27 / augusto.rueda@ufes.br