Análise de Sistemas de Energia Elétrica
Departamento de Engenharia Elétrica
Unidade 7
Faltas Trifásicas Simétricas e Assimétricas
Faltas Trifásicas Simétricas
Faltas Trifásicas Simétricas - Introdução
O problema formulado nos estudos de curto-circuito consiste, principalmente, na determinação das tensões e correntes nas linhas durante uma falta.
Os tipos de curto-circuito em um sistema de energia elétrica são divididos em curto-circuito trifásicos simétricos e assimétricos.
A informação obtida dos estudos de curto-circuito é usada para selecionar e coordenar apropriadamente os sistemas de proteção.
Enquanto que os diagramas unifilares simplificam os estudos de curto-circuito do tipo simétrico, o método das componentes simétricas é utilizado para resolver o problema de curto-circuito do tipo assimétrico.
Faltas Trifásicas Simétricas - Introdução
Tipos de curto-circuito:
Curto-circuito simétrico: curto-circuito simultâneo através das três fases ou através das três fases e terra.
Curto-circuito assimétrico:
Curto-circuito entre fase e terra.
Curto-circuito entre duas fases.
Curto-circuito entre duas fases e terra.

Faltas Trifásicas Simétricas - Introdução
Causas de curto-circuito:
Contatos momentâneos entre condutores.
Aves, roedores, galhos de árvores.
Rigidez dielétrica afetada por frio ou calor.
Descargas atmosféricas.
Danos nos equipamentos devido à umidade e corrosão.

Faltas Trifásicas Simétricas - Introdução
Principais consequências de um curto-circuito:
Danos por efeitos dinâmicos e térmicos.
Descontinuidade do fornecimento de energia.
Possível presença de arcos elétricos.
Danos à isolação dos condutores.
Aumento das perdas Joule.
Faltas Trifásicas Simétricas - Introdução
Principais consequências de um curto-circuito:
Aumento das perdas Joule.
Instabilidade dinâmica e/ou a perda de sincronização de máquinas síncronas.
Distúrbios em circuitos do controle/monitoração.
Possível presença de fogo.
Danos físicos em equipamentos.
Faltas Trifásicas Simétricas - Definição
Definido como curto-circuito simultâneo entre todas as três fases (cou ou sem terra).
Em razão de que o sistema é considerado balanceado, este problema é resolvido em uma base pu.
A reatância de um gerador síncrono sob situação de curto-circuito é uma quantidade que varia no tempo e, para análise, são definidas três reatâncias:
Reatância subtransitória $\small X^{''}_d$: primeiros poucos ciclos da corrente de curto-circuito;
reatância transitória $\small X^{'}_d$: pelos próximmos trinta ciclos da corrente de curto-circuito;
reatância síncrona $\small X_d$: daí em diante.
Nem sempre é fácil decidir qual reatância usar. Geralmente, são usadas as reatâncias subtransitíria (determinar capacidade de interrupção do circuito) e transitória (configuração e coordenação de relés).
Faltas Trifásicas Simétricas - Método Básico
Um curto-circuito representa uma mudança estrutural da rede que pode ser representada pela adição de uma impedância no lugar da falta, a impedância de falta $\small {Z}_F$.

Faltas Trifásicas Simétricas - Método Básico
A rede em falta pode ser resolvida usando unicamente um circuito equivalente de Thèvenin.
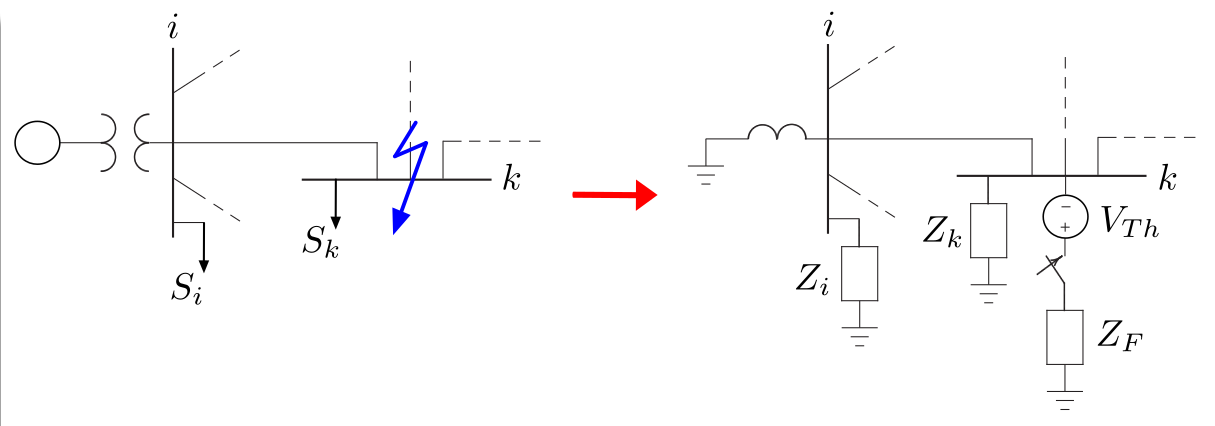
Faltas Trifásicas Simétricas - Método Básico - Exemplo 7.1.1
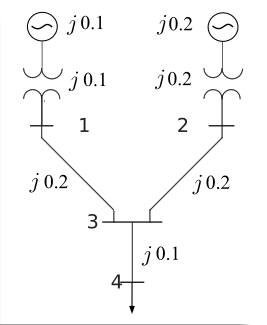
Considere-se uma falta na barra 4 do circuito da figura acima. $\small \Delta{V}_{4}$=?
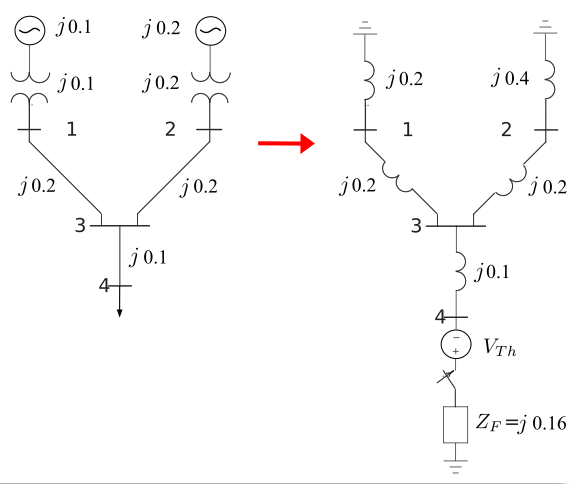
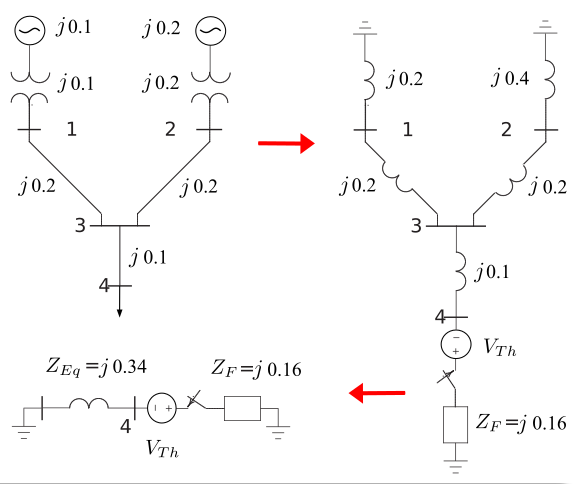
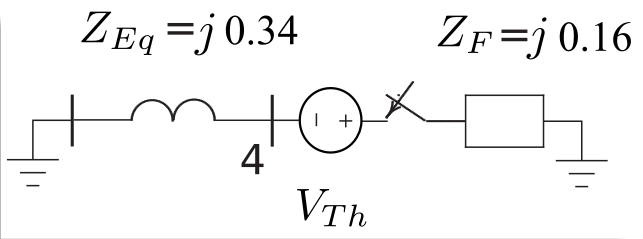
Sabendo-se que $\small {V}_{\rm{Th}}=1$ pu:
$\small {I}_{\rm{F}} = \frac{{{V}_{\rm{Th}} }}{{{Z}_{\rm{Eq}} + {Z}_{\rm{F}} }} = \frac{1}{{j0.34 + j0.16}}{\rm{pu}} = - j2{\rm{pu}}$
A variação da tensão na barra 4 , $\small \Delta{V}_{4}$, é:
$\small \Delta{V}_{4} = {Z}_{\rm{Eq}}{I}_{\rm{F}} = j 0.34 \left({ -j2 } \right) {\rm{pu}}= 0.68 {\rm{pu}}$
Assim:
$\small {V}_{4,{\rm{F}}} = {V}_{4,{\rm{Pre}}} + \Delta{V}_{4}$
Faltas Trifásicas Simétricas - Método da Matriz Impedância de Barra
Uma forma geral de análise de circuitos em falta é através do uso da matria impedância de barra $\small {Z}_{\rm{Barra}}$.
Supondo que as tensões de pré-falta, $\small {V}_{\rm{Barra}} \left( 0 \right)$ e as variações das tensões, $\small \Delta{V}_{\rm{Barra}}$, causadas pelo curto-circuito são:
$\scriptsize {V}_{\rm{Barra}} \left( 0 \right) = \left[ {\begin{array}{*{20}c} {{V}_1 \left( 0 \right)} \\ \vdots \\ {{V}_{\rm{k}} \left( 0 \right)} \\ \vdots \\ {{V}_{\rm{n}} \left( 0 \right)} \\ \end{array}} \right] \hspace{1cm} \Delta{V}_{\rm{Barra}} = \left[ {\begin{array}{*{20}c} {\Delta{V}_1 } \\ \vdots \\ {\Delta{V}_{\rm{k}} } \\ \vdots \\ {\Delta{V}_{\rm{n}} } \\ \end{array}} \right] $
Por superposição, tem-se que:
$\scriptsize {V}_{\rm{F,Barra}} = {V}_{\rm{Barra}} \left( 0 \right) + \Delta{V}_{\rm{Barra}} $
Faltas Trifásicas Simétricas - Método da Matriz Impedância de Barra
Sabendo-se que:
$\small {I}_{\rm{Barra}} = {Y}_{\rm{Barra}} {V}_{\rm{Barra}} \\ \small \Rightarrow {I}_{\rm{F,Barra}} = {Y}_{\rm{Barra}} \Delta{V}_{\rm{Barra}} \\ \small \Delta{V}_{\rm{Barra}} = \left({{Y}_{\rm{Barra}}}\right)^{-1} {I}_{\rm{F,Barra}} = {Z}_{\rm{Barra}} {I}_{\rm{F,Barra}} $
Em forma matricial:
$\scriptsize \left[ {\begin{array}{*{20}c} { \Delta {V}_1} \\ \vdots \\ {{\Delta {V}_{\rm{k}} }} \\ \vdots \\ {\Delta {V}_{\rm{n}} } \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {{Z}_{11} } & \cdots & {{Z}_{1{\rm{k}}} } & \cdots & {{Z}_{1{\rm{n}}} } \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {{Z}_{{\rm{k}}1} } & \cdots & {{{Z}_{{\rm{kk}}} }} & \cdots & {{Z}_{{\rm{kn}}} } \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {{Z}_{{\rm{n}}1} } & \cdots & {{Z}_{{\rm{nk}}} } & \cdots & {{Z}_{{\rm{nn}}} } \\ \end{array}} \right]\left[ {\begin{array}{*{20}c} 0 \\ \vdots \\ {{ - {I}_{{\rm{F,k}}} }} \\ \vdots \\ 0 \\ \end{array}} \right] $
$\small \Delta{V}_{\rm{k}} = - {Z}_{\rm{kk}}{I}_{\rm{F,k}} $
Faltas Trifásicas Simétricas - Método da Matriz Impedância de Barra
$\scriptsize \Delta{V}_{\rm{k}} = - {Z}_{\rm{kk}}{I}_{\rm{F,k}} $
$\scriptsize {V}_{\rm{F,k}} = {V}_{\rm{k}} \left( 0 \right) + \Delta{V}_{\rm{k}} \Rightarrow {{{V}_{\rm{F,k}} = {V}_{\rm{k}} \left( 0 \right) - {Z}_{\rm{kk}}{I}_{\rm{F,k}}}} $
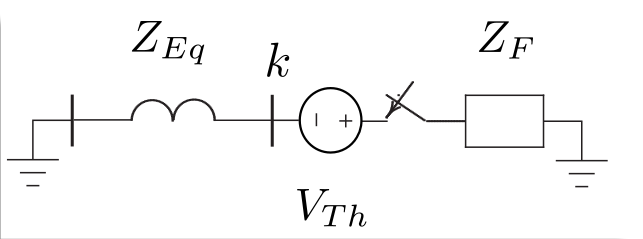
Do circuito equivalente de Thèvenin:
$\scriptsize {V}_{\rm{F,k}} = {Z}_{\rm{F}} {I}_{\rm{F,k}} $
$\scriptsize {{V}_{\rm{k}} \left( 0 \right) - {Z}_{\rm{kk}}{I}_{\rm{F,k}} = {Z}_{\rm{F}} {I}_{\rm{F,k}} \Rightarrow} {{ {I}_{\rm{F,k}} = \frac{{V}_{\rm{k}} \left( 0 \right)}{{Z}_{\rm{F}} + {Z}_{\rm{kk}}}}} $
Faltas Trifásicas Simétricas - Método da Matriz Impedância de Barra - Exemplo 7.1.2

Determinar a corrente e tensões de falta usando a matriz $\small {Z}_{\rm{Barra}}$.
Sabendo-se que a matiz $\small {Z}_{\rm{Barra}}$ é:
$\scriptsize {Z}_{\rm{Barra}} = \left[ {\begin{array}{*{20}c} {j 0,16 } & j 0,08 & j 0,12 \\ j 0,08 & j 0,24 & j 0,16 \\ j 0,12 & j 0,16 & j 0,34 \end{array}} \right] $
e que $\small {Z}_{\rm{F}} = j 0,16$, tem-se que:
$\scriptsize {{ {I}_{\rm{F,k}} = \frac{{V}_{\rm{k}} \left( 0 \right)}{{Z}_{\rm{F}} + {Z}_{\rm{kk}}}}} = {I}_{\rm{F,3}} = \frac{{V}_{\rm{3}} \left( 0 \right)}{{Z}_{\rm{F}} + {Z}_{\rm{33}}} = \frac{1,0 \left( 0 \right)}{j 0,16 + j 0,34} = -j 2,0 $
$\scriptsize {V}_{\rm{1}} = {V}_{\rm{1}} \left( 0 \right) - {Z}_{\rm{13}} {I}_{\rm{F,3}} = 1,0 - j 0,12 (- j 2,0) = 0,76 $ pu
$\scriptsize {V}_{\rm{2}} = {V}_{\rm{2}} \left( 0 \right) - {Z}_{\rm{23}} {I}_{\rm{F,3}} = 1,0 - j 0,16 (- j 2,0) = 0,68 $ pu
$\scriptsize {V}_{\rm{3}} = {V}_{\rm{3}} \left( 0 \right) - {Z}_{\rm{33}} {I}_{\rm{F,3}} = 1,0 - j 0,34 (- j 2,0) = 0,32 $ pu
Análise de Sistemas de Energia Elétrica
Departamento de Engenharia Elétrica

