Análise de Sistemas de Energia Elétrica

Departamento de Engenharia Elétrica

Prof. Augusto César Rueda Medina / CT-XI, Sala 27 / augusto.rueda@ufes.br

Unidade 3

3.1. Solução de Equações Algébricas Não-lineares

Solução de Equações Algébricas Não-lineares

As técnicas mais comumente utilizadas para solução de equações agébricas não-lineares são os métodos Gaus-Seidel, Newton-Raphson e Quase-Newton.
Inicialmente, serão apresentandos os métodos Gaus-Seidele Newton-Raphson unidimensionais e, seguidamente, serão extendidos a equações $\small n$-dimensionais.

Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel

O método Gauss-Seidel também é conhecido como "Método de deslocamentos sucessivos".

Para ilustrar a técnica, considere a solução da equação não-linear dada por:

$\small f(x) = 0$

A anterior função é rearanjada e escrita como:

$\small x = g(x)$

Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel

Se $\small x^{(k)}$ é uma aproximação inicial da variável $\small x$, então é formada a seguinte sequência iterativa:

$\small x^{(k+1)} = g \left({ x^{(k)} }\right) $

A solução é obtida quando a diferença entre o valor absoluto de uma iteração sucessiva é menor que uma tolerância especificada $\small \epsilon$, isto é:

$\small | x^{(k+1)} - x^{(k)} | \leq \epsilon$

Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel - Exemplo 3.1.1

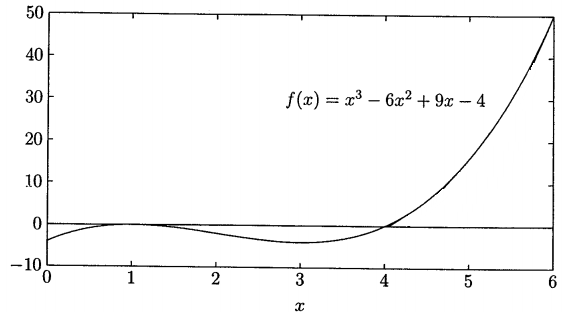
Usar o Método Gauss-Seidel, considerando como solução inicial $\small x^{(0)} = 2$ (no intervalo 1 a 4), para determinar a raiz da seguinte equação:

$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$

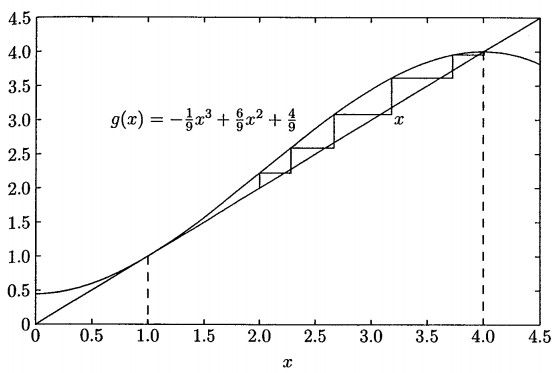
Resolvendo para $\small x$, a expressão anterior é escrita como:

$\small x = -\frac{1}{9}x^3 + \frac{6}{9}x^2 + \frac{4}{9} $

$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$

Resolvendo para $\small x$, a expressão anterior é escrita como:

$\small x = -\frac{1}{9}x^3 + \frac{6}{9}x^2 + \frac{4}{9} $

A primeira iteração é:

$\small x^{(1)} = g(x^{(0)}) = g(2) = -\frac{1}{9}2^3 + \frac{6}{9}2^2 + \frac{4}{9} = 2,2222$

A segunda iteração é:

$\small x^{(2)} = g(x^{(1)}) = g(2.2222) = -\frac{1}{9}2.2222^3 + \frac{6}{9}2.2222^2 + \frac{4}{9} = 2,5173$

As subsequentes iterações resultam em 2.8966, 3.3376, 3.7398, 3.9568, 3.9988 e 4.0000 . O processo é repetido até que a mudança na variável esteja dentro da tolerância desejada.

Pode ser observado que o Método Gauss-Seidel precisa de muitas iterações para alcançar a precisão desejada. Além disso, não há garantia de convergência.

Neste exemplo, dado que a solução inicial ($\small x^{(0)} = 2$) está em uma região "fechada", a solução converge em forma de "zigzag" a uma das raízes.

De fato, se a estimativa inicial estivesse fora do intervalo definido 1 a 4, $\small x^{(0)} = 6$, por exemplo, o processo divergiria.

Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel

Considerando agora um sistema de $\small n$ equações não-lineares com $\small n$ incógnitas:

$\small \begin{array}{*{20}{c}} {{f_1}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_1}}\\ {{f_2}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_2}}\\ \vdots \\ {{f_n}\left( {{x_1},{x_2}, \ldots ,{x_n}} \right) = {c_n}} \end{array} $

Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel

Resolvendo para cada equação, as funções acima são rearranjadas e escritas como:

$\small \begin{array}{*{20}{c}} {{x_1} = c_1 + g_1\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)}\\ {{x_2} = c_2 + g_2\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)}\\ \vdots \\ {{x_n} = c_n + g_n\left( {{x_1},{x_2}, \ldots ,{x_n}} \right)} \end{array} $

Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel

O processo iterativo é iniciado assumindo uma solução aproximada para cada variável independentemente ($\small x_1^{(0)}$, $\small x_2^{(0)}$, $\small \cdots$, $\small x_n^{(0)}$).

A solução do sistema de equações anterior resulta em uma nova aproximação ($\small x_1^{(1)}$, $\small x_2^{(1)}$, $\small \cdots$, $\small x_n^{(1)}$).

Solução de Equações Algébricas Não-lineares - Método Gauss-Seidel

No método Gauss-Seidel, os valores atualizados das variáveis calculadas nas anteriores equações são imediatamente usados na solução das equações subsequentes.

No final de cada iteração, os valores calculados de todas as variáveis são comparados com seus correspondentes valores prévios. Se todas as mudanças nas variáveis estão dentro da tolerância especificada, a solução tem convergido.

A velocidade de convergência pode ser incrementada usando um fator de aceleração $\small \alpha$, e a iteração subsequente fica:

$\small x_i^{(k + 1)} = x_i^{(k)} + \alpha ( x_{i,calc}^{(k + 1)} - x_i^{(k)})$

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

O método mais amplamente usado para resolver equações algébricas não-lineares simultâneas é o Método de Newton-Raphson.

Este método consiste em processo sucessivo de aproximações baseadas em uma estimativa inicial e o uso da expansão em séries de Taylor.

Considere a solução do da equação unidimensional dada por:

$\small f(x) = c$

Se $\small x^{(0)}$ é a aproximação inicial da solução, e $\small \Delta x^{(0)}$ é um pequeno desvio da solução correta, então:

$\small f(x^{(0)} + \Delta x^{(0)}) = c$

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

$\small f(x^{(0)} + \Delta x^{(0)}) = c$

Expandindo o lado esquerdo da anterior expressão em séries de Taylor em torno de $\small x^{(0)}$:

$\small f(x^{(0)}) + \left({\frac{df}{dx}}\right) ^{(0)}\Delta x^{(0)} + \frac{1}{2!}\left({\frac{d^2f}{dx^2}}\right)^{(0)}\Delta (x^{(0)})^2 + \cdots = c$

Assumindo que o erro $\small \Delta x^{(0)}$ seja muito pequeno, os termos de ordem superior podem ser desprezados, o que resulta em:

$\small \Delta c^{(0)} \simeq \left({\frac{df}{dx}}\right) ^{(0)}\Delta x^{(0)}$

Sendo:

$\small \Delta c^{(0)} = c - f(x^{(0)})$

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

$\small \Delta c^{(0)} \simeq \left({\frac{df}{dx}}\right) ^{(0)}\Delta x^{(0)}$

Sendo:

$\small \Delta c^{(0)} = c - f(x^{(0)})$

Adicionando $\small \Delta x^{(0)}$ à apriximação inicial, resultará na segunda aproximação:

$\small x^{(1)} = x^{(0)} + \frac{\Delta c^{(0)}}{\left({\frac{df}{dx}}\right)^{(0)}}$

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

$\small x^{(1)} = x^{(0)} + \frac{\Delta c^{(0)}}{\left({\frac{df}{dx}}\right)^{(0)}}$

O uso sucessivo da anterior expressão leva ao algoritmo de Newton-Raphson:

$\small \Delta c^{(k)} = c - f(x^{(k)})$

$\small \Delta x^{(k)} = \frac{\Delta c^{(k)}}{\left({\frac{df}{dx}}\right)^{(k)}}$

$\small x^{(k+1)} = x^{(k)} + \Delta x^{(k)}$

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

$\small \Delta c^{(k)} = c - f(x^{(k)})$

$\small \Delta x^{(k)} = \frac{\Delta c^{(k)}}{\left({\frac{df}{dx}}\right)^{(k)}}$

$\small x^{(k+1)} = x^{(k)} + \Delta x^{(k)}$

As anteriores expressões podem ser rearranjadas como:

$\small \Delta c^{(k)} = j^{(k)} \Delta x^{(k)}$

$\small j^{(k)} = \left({\frac{df}{dx}}\right)^{(k)}$

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

$\small \Delta c^{(k)} = j^{(k)} \Delta x^{(k)}$

$\small j^{(k)} = \left({\frac{df}{dx}}\right)^{(k)}$

A relação anterior demonstra que a equação não-linear $\small f(x) - c = 0$ é aproximada pela linha tangente à curva no ponto $\small x^{(k)}$. Assim, é obtida uma equação linear em termos de pequenas mudanças na variável.

A interseção da linha tangente no ponto $\small x^{(k)}$ com o eixo $\small x$ resulta em $\small x^{(k + 1)}$. Esta ideia é demonstrada graficamente no exemplo a seguir.

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson - Exemplo 3.1.2

Usar o Método Newton-Raphson, considerando como solução inicial $\small x^{(0)} = 6$, para determinar a raiz da seguinte equação:

$\small f(x) = x^3 - 6x^2 + 9x -4 = 0$

A derivada de $\small f(x)$ é:

$\small \frac{df(x)}{dx} = 3x^2 - 12x + 9$

Na primeira iteração, $\Delta c^{(0)}$ é:

$\small \Delta c^{(0)} = c - f(x^{(0)}) = 0 - 50 = -50$

$\small \left({\frac{df}{dx}}\right)^{(0)} = 45$

$\small \Delta x^{(0)} = \frac{\Delta c^{(0)}}{\left({\frac{df}{dx}}\right)^{(0)}} = \frac{-50}{45} = -1,1111$

Assim, o resultado no final da primeira iteração é:

$\small x^{(1)} = x^{(0)} + \Delta x^{(0)} = 6 - 1,1111 = 4,8889$

Nas iterações subsequentes resultam em:

$\small x^{(2)} = x^{(1)} + \Delta x^{(1)} = 4,8889 - \frac{13,4431}{22,037} = 4,2789$

$\small x^{(3)} = x^{(2)} + \Delta x^{(2)} = 4,2789 - \frac{2,9981}{12,5797} = 4,0405$

$\small x^{(4)} = x^{(3)} + \Delta x^{(3)} = 4,0405 - \frac{0,3748}{9,4914} = 4,0011$

$\small x^{(5)} = x^{(4)} + \Delta x^{(4)} = 4,0011 - \frac{0,0095}{9,0126} = 4,0000$

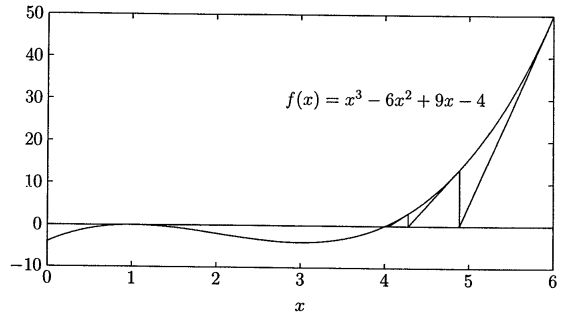
Pode ser observado que o Método de Newton-Raphson converge consideravelmente mais rapidamente que o Método Gauss-Seidel.

O Método de Newton-Raphson pode convergir a uma raiz diferente da esperada ou então divergir se a aproximação inicial não está o suficientemente próxima da raiz.

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

Considere agora o seguinte conjunto $\small n$ dimensional de equações:

$\small \begin{array}{*{20}{c}} {{{\left( {{f_1}} \right)}^{(0)}} + {{\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}}} \right)}^{(0)}}\Delta x_1^{(0)} + {{\left( {\frac{{\partial {f_1}}}{{\partial {x_2}}}} \right)}^{(0)}}\Delta x_2^{(0)} + \cdots + {{\left( {\frac{{\partial {f_1}}}{{\partial {x_n}}}} \right)}^{(0)}}\Delta x_n^{(0)} = {c_1}}\\ {{{\left( {{f_2}} \right)}^{(0)}} + {{\left( {\frac{{\partial {f_2}}}{{\partial {x_1}}}} \right)}^{(0)}}\Delta x_1^{(0)} + {{\left( {\frac{{\partial {f_2}}}{{\partial {x_2}}}} \right)}^{(0)}}\Delta x_2^{(0)} + \cdots + {{\left( {\frac{{\partial {f_2}}}{{\partial {x_n}}}} \right)}^{(0)}}\Delta x_n^{(0)} = {c_2}}\\ \vdots \\ {{{\left( {{f_n}} \right)}^{(0)}} + {{\left( {\frac{{\partial {f_n}}}{{\partial {x_1}}}} \right)}^{(0)}}\Delta x_1^{(0)} + {{\left( {\frac{{\partial {f_n}}}{{\partial {x_2}}}} \right)}^{(0)}}\Delta x_2^{(0)} + \cdots + {{\left( {\frac{{\partial {f_n}}}{{\partial {x_n}}}} \right)}^{(0)}}\Delta x_n^{(0)} = {c_n}} \end{array}$

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

Ou na forma matricial:

$\scriptsize \left[ {\begin{array}{*{20}{c}} {{c_1} - {{\left( {{f_1}} \right)}^{(0)}}}\\ {{c_2} - {{\left( {{f_2}} \right)}^{(0)}}}\\ \vdots \\ {{c_n} - {{\left( {{f_n}} \right)}^{(0)}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}}} \right)}^{(0)}}}&{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_{2}}}}} \right)}^{(0)}}}& \cdots &{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_n}}}} \right)}^{(0)}}}\\ {{{\left( {\frac{{\partial {f_2}}}{{\partial {x_1}}}} \right)}^{(0)}}}&{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_{2}}}}} \right)}^{(0)}}}& \cdots &{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_n}}}} \right)}^{(0)}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{{\left( {\frac{{\partial {f_n}}}{{\partial {x_1}}}} \right)}^{(0)}}}&{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_{2}}}}} \right)}^{(0)}}}& \cdots &{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_n}}}} \right)}^{(0)}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta x_1^{(0)}}\\ {\Delta x_2^{(0)}}\\ \vdots \\ {\Delta x_n^{(0)}} \end{array}} \right]$

Em forma compacta, pode ser escrito como:

$\small \Delta C^{(k)} = J^{(k)} \Delta X^{(k)}$

$\small \Delta X^{(k)} = \left[{ J^{(k)} }\right] ^{-1} \Delta C^{(k)} $

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

$\small \Delta X^{(k)} = \left[{ J^{(k)} }\right] ^{-1} \Delta C^{(k)} $

A atualização das variáveis usando o Método de Newton-Raphson, para o sistema $\small n$ dimensional, fica então:

$\small X^{(k + 1)} = X^{(k)} + \Delta X^{(k)} $

Sendo:

$\tiny \Delta {X^{(k)}} = \left[ {\begin{array}{*{20}{c}} {\Delta x_1^{(k)}}\\ {\Delta x_2^{(k)}}\\ \vdots \\ {\Delta x_n^{(k)}} \end{array}} \right];{\rm{ }}\Delta {C^{(k)}} = \left[ {\begin{array}{*{20}{c}} {{c_1} - {{\left( {{f_1}} \right)}^{(k)}}}\\ {{c_2} - {{\left( {{f_2}} \right)}^{(k)}}}\\ \vdots \\ {{c_n} - {{\left( {{f_n}} \right)}^{(k)}}} \end{array}} \right];{\rm{ }}{J^{(k)}} = \left[ {\begin{array}{*{20}{c}} {{{\left( {\frac{{\partial {f_1}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_1}}}{{\partial {x_n}}}} \right)}^{(k)}}}\\ {{{\left( {\frac{{\partial {f_2}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_2}}}{{\partial {x_n}}}} \right)}^{(k)}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{{\left( {\frac{{\partial {f_n}}}{{\partial {x_1}}}} \right)}^{(k)}}}&{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_{2}}}}} \right)}^{(k)}}}& \cdots &{{{\left( {\frac{{\partial {f_n}}}{{\partial {x_n}}}} \right)}^{(k)}}} \end{array}} \right]$

Solução de Equações Algébricas Não-lineares - Método Newton-Raphson

$\small J^{(k)}$ é chamada de Matriz Jacobiana. Os elementos desta matriz são as derivadas parciais avaliadas no ponto $\small X^{(k)}$.

É assumido que $\small J^{(k)}$ tem inversa em cada iteração.

O Método de Newton-Raphson, quando aplicado a um conjunto de equações não-lineares, reduz o problema à resolução de um sistema de equações lineares.

Análise de Sistemas de Energia Elétrica

Departamento de Engenharia Elétrica

Prof. Augusto César Rueda Medina / CT-XI, Sala 27 / augusto.rueda@ufes.br