Análise de Sistemas de Energia Elétrica

Universidade Federal do Espírito Santo

Departamento de Engenharia Elétrica

Prof. Augusto César Rueda Medina / CT-XI, Sala 27 / augusto.rueda@ufes.br

Unidade 2

2.2. Ramos Mutuamente Acoplados e Modificações na Matriz Admitância de Barra

Ramos Mutuamente Acoplados na Matriz Admitância de Barra

Na figura a seguir, mostra-se um trecho de circuito em que existe admitância ou impedância mútua entre alguns elementos do sistema elétrico:

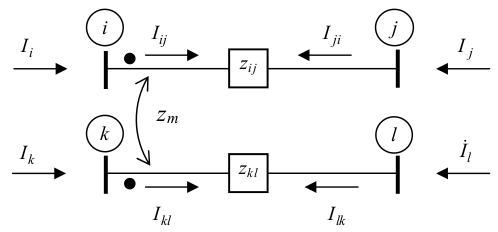
Neste circuito, a polaridade da tensão induzida é importante.

Ramos Mutuamente Acoplados na Matriz Admitância de Barra

Polaridade relativa da corrente:

$\small V_i - V_j = z_{ij} I_{ij} + z_{m} I_{kl}$

$\small V_k - V_l = z_{kl} I_{kl} + z_{m} I_{ij}$

Ramos Mutuamente Acoplados na Matriz Admitância de Barra

$\small V_i - V_j = z_{ij} I_{ij} + z_{m} I_{kl}$

$\small V_k - V_l = z_{kl} I_{kl} + z_{m} I_{ij}$

De forma matricial:

$\small \left[ \begin{array}{l} {V_i} - {V_j}\\ {V_k} - {V_l} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{z_{ij}}}&{{z_m}}\\ {{z_m}}&{{z_{kl}}} \end{array}} \right]\left[ \begin{array}{l} {I_{ij}}\\ {I_{kl}} \end{array} \right]$

A matriz $\small Z$ é chamada de matriz impedância primitiva do elemento.

Ramos Mutuamente Acoplados na Matriz Admitância de Barra

Passando-se para admitância:

$\small \left[ \begin{array}{l} {I_{ij}}\\ {I_{kl}} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{y_{ij}}}&{{y_m}}\\ {{y_m}}&{{y_{kl}}} \end{array}} \right]\left[ \begin{array}{l} {V_i} - {V_j}\\ {V_k} - {V_l} \end{array} \right]$

A matriz $\small Y$ é chamada de matriz admitância primitiva do elemento.

Ramos Mutuamente Acoplados na Matriz Admitância de Barra

Expandindo a equação acima:

$\small I_{ij} = y_{ij} V_i - y_{ij} V_j + y_{m} V_{k} - y_{m} V_{l}$

$\small I_{ji} = - y_{ij} V_i + y_{ij} V_j - y_{m} V_{k} + y_{m} V_{l}$

$\small I_{kl} = y_{m} V_i - y_{m} V_j + y_{kl} V_{k} - y_{kl} V_{l}$

$\small I_{lk} = - y_{m} V_i + y_{m} V_j - y_{kl} V_{k} + y_{kl} V_{l}$

Ramos Mutuamente Acoplados na Matriz Admitância de Barra

$\small I_{ij} = y_{ij} V_i - y_{ij} V_j + y_{m} V_{k} - y_{m} V_{l}$

$\small I_{ji} = - y_{ij} V_i + y_{ij} V_j - y_{m} V_{k} + y_{m} V_{l}$

$\small I_{kl} = y_{m} V_i - y_{m} V_j + y_{kl} V_{k} - y_{kl} V_{l}$

$\small I_{lk} = - y_{m} V_i + y_{m} V_j - y_{kl} V_{k} + y_{kl} V_{l}$

Sabendo que $\small I_{ij} = I_i$, $\small I_{ji} = I_j$, $\small I_{kl} = I_k$, $\small I_{lk} = I_l$:

$\small \left[ \begin{array}{l} {I_{i}}\\ {I_{j}}\\ {I_{k}}\\ {I_{l}} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{y_{ij}}}&{{-y_{ij}}}&{{y_{m}}}&{{-y_{m}}}\\ {{-y_{ij}}}&{{y_{ij}}}&{{-y_{m}}}&{{y_{m}}}\\ {{y_{m}}}&{{-y_{m}}}&{{y_{kl}}}&{{-y_{kl}}}\\ {{-y_{m}}}&{{y_{m}}}&{{-y_{kl}}}&{{y_{kl}}} \end{array}} \right]\left[ \begin{array}{l} {V_i}\\ {V_j}\\ {V_k}\\ {V_l} \end{array} \right]$

Ramos Mutuamente Acoplados na Matriz Admitância de Barra

Regra prática para a montagem da matriz $\small Y_{\rm{Barra}}$ com acoplamentos:

Determinar a matriz $\small Z$ primitiva dos elementos com acoplamento.
Inverter a matriz $\small Z$ primitiva do elemento para encontrar a matriz $\small Y$ primitiva.
Montar a matriz $\small Y_{\rm{Barra}}$ sem considerar a admitância mútua $\small y_m$.
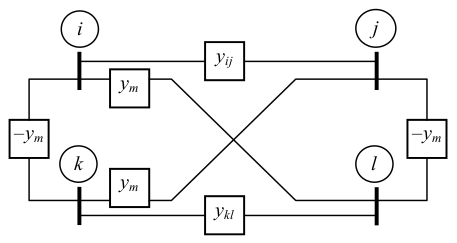
Incluir o efeito dos acoplamentos somando $\small y_m$ aos elementos da matriz referentes aos terminais igualmente marcados e subtraindo $\small y_m$ dos elementos da matriz eferentes aos terminais marcados diferentemente.

Ramos Mutuamente Acoplados na Matriz Admitância de Barra

Matriz Admitância de Barra com Acoplamentos - Exemplo 2.2.1

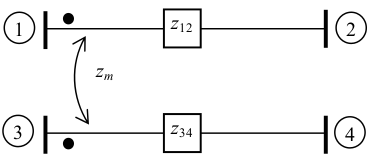
Sejam $\small z_{12} = z_{34} = j0,25$ pu e $\small z_m = j0,15$, como mostrados na figura. Determinar a matriz $\small Y_{\rm{Barra}}$ do sistema.

Diferença de tensão entre as barras:

$\small \left[ \begin{array}{l} {V_1} - {V_2}\\ {V_3} - {V_4} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {j0,25}&{j0,15}\\ {j0,15}&{j0,25} \end{array}} \right]\left[ \begin{array}{l} {I_{12}}\\ {I_{34}} \end{array} \right]$

Inversa da matriz $\small Z$ primitiva, $\small Y$ primitiva:

$\small Y = \left[ {\begin{array}{*{20}{c}} {-j6,25}&{j3,75}\\ {j3,75}&{-j6,25} \end{array}} \right]$

$\small y_m = j3,75$ pu, $\small y_{12} = y_{34} = -j6,25$ pu.

Matriz $\small Y_{\rm{Barra}}$ sem acoplamento:

$\small Y_{\rm{Barra}} = \left[ {\begin{array}{*{20}{c}} {-j6,25}&{j6,25}&{0}&{0}\\ {j6,25}&{-j6,25}&{0}&{0}\\ {0}&{0}&{-j6,25}&{j6,25}\\ {0}&{0}&{j6,25}&{-j6,25} \end{array}} \right]$

Matriz $\small Y_{\rm{Barra}}$ com acoplamento:

$\small Y_{\rm{Barra}} = \left[ {\begin{array}{*{20}{c}} {-j6,25}&{j6,25}&{j3,75}&{-j3,75}\\ {j6,25}&{-j6,25}&{-j3,75}&{j3,75}\\ {j3,75}&{-j3,75}&{-j6,25}&{j6,25}\\ {-j3,75}&{j3,75}&{j6,25}&{-j6,25} \end{array}} \right]$

Matriz $\small Y_{\rm{Barra}}$ com acoplamento:

$\scriptsize Y_{\rm{Barra}} = \left[ {\begin{array}{*{20}{c}} {-j6,25}&{j6,25}&{j3,75}&{-j3,75}\\ {j6,25}&{-j6,25}&{-j3,75}&{j3,75}\\ {j3,75}&{-j3,75}&{-j6,25}&{j6,25}\\ {-j3,75}&{j3,75}&{j6,25}&{-j6,25} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{y_{ij}}}&{{-y_{ij}}}&{{y_{m}}}&{{-y_{m}}}\\ {{-y_{ij}}}&{{y_{ij}}}&{{-y_{m}}}&{{y_{m}}}\\ {{y_{m}}}&{{-y_{m}}}&{{y_{kl}}}&{{-y_{kl}}}\\ {{-y_{m}}}&{{y_{m}}}&{{-y_{kl}}}&{{y_{kl}}} \end{array}} \right]$

Incluir o efeito dos acoplamentos somando $\small y_m$ aos elementos da matriz referentes aos terminais igualmente marcados e subtraindo $\small y_m$ dos elementos da matriz eferentes aos terminais marcados diferentemente.

Matriz Admitância de Barra com Acoplamentos - Exemplo 2.2.2

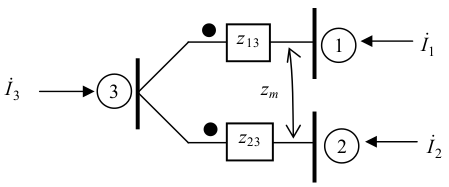
Sejam $\small z_{13} = z_{23} = j0,25$ pu e $\small z_m = j0,15$, como mostrados na figura. Determinar a matriz $\small Y_{\rm{Barra}}$ do sistema.

Matriz $\small Z$ primitiva:

$\small Z = \left[ {\begin{array}{*{20}{c}} {j0,25}&{j0,15}\\ {j0,15}&{j0,25} \end{array}} \right]$

Inversa da matriz $\small Z$ primitiva, $\small Y$ primitiva:

$\small Y = \left[ {\begin{array}{*{20}{c}} {-j6,25}&{j3,75}\\ {j3,75}&{-j6,25} \end{array}} \right]$

$\small y_m = j3,75$ pu, $\small y_{13} = y_{23} = -j6,25$ pu.

Matriz $\small Y_{\rm{Barra}}$ sem acoplamento:

$\small Y_{\rm{Barra}} = \left[ {\begin{array}{*{20}{c}} {-j6,25}&{0}&{j6,25}\\ {0}&{-j6,25}&{j6,25}\\ {j6,25}&{j6,25}&{-j12,5=-j6,25-j6,25} \end{array}} \right]$

Matriz $\small Y_{\rm{Barra}}$ com acoplamento:

$\tiny Y_{\rm{Barra}} = \left[ {\begin{array}{*{20}{c}} {-j6,25}&{0 + j3,75}&{j2,5 = j6,25 - j3,75}\\ {0 + j3,75}&{-j6,25}&{j2,5 = j6,25 - j3,75}\\ {j2,5 = j6,25 - j3,75}&{j2,5 = j6,25 - j3,75}&{-j5=-j12,5+j3,75+j3,75} \end{array}} \right]$

Matriz $\small Y_{\rm{Barra}}$ com acoplamento:

Modificações na Matriz Admitância de Barra

As matrizes impedância de barra e admitância de barra de um sistema elétrico real são muito grandes, dimensão da ordem de milhares.
Em alguns estudos, não é necessário conhecer a tensão em todas as barras do sistema, logo são usadas técnicas para reduzir a dimensão da rede, eliminando-se trechos não prioritários para o estudo em questão.

Modificações na Matriz Admitância de Barra - Eliminação de Barras

Seja a rede elétrica representada pela matriz admitância de barra $\small Y_{\rm{Barra}}$. A eliminação se processa para duas diferentes situações:

Não existe fonte de corrente na barra a ser eliminada.
Existe fonte de corrente na barra a ser eliminada.

Modificações na Matriz Admitância de Barra - Eliminação de Barras sem Fonte de Corrente

Particionamento da matriz. Ordenam-se as equações de tal forma que todas as barras sem fonte fiquem juntas e na parte inferior da matriz.

$\small \left[ {\begin{array}{*{20}{c}} {{I_1}}\\ {{I_2}}\\ {{I_3}}\\ \cdots \\ {{I_4}}\\ {{I_5}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {}& \vdots &{}\\ {{Y_{AA}}}& \vdots &{{Y_{AB}}}\\ {}& \vdots &{}\\ { \cdots \cdots \cdots }& \cdots & \cdots \\ {{Y_{BA}} = Y_{AB}^T}& \vdots &{{Y_{BB}}}\\ {}& \vdots &{} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{V_2}}\\ {{V_3}}\\ \cdots \\ {{V_4}}\\ {{V_5}} \end{array}} \right] $

Modificações na Matriz Admitância de Barra - Eliminação de Barras sem Fonte de Corrente

$\small \left[ \begin{array}{l} {I_A}\\ {I_B} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{Y_{AA}}}&{{Y_{AB}}}\\ {Y_{AB}^T}&{{Y_{BB}}} \end{array}} \right]\left[ \begin{array}{l} {V_A}\\ {V_B} \end{array} \right] $

Modificações na Matriz Admitância de Barra - Eliminação de Barras sem Fonte de Corrente

Supondo $\small I_B = 0$:

$\small I_A = Y_{AA} V_A + Y_{AB} V_B $

$\small I_B = Y_{AB}^T V_A + Y_{BB} V_B = 0 $

$\small \Rightarrow V_B = -Y_{BB}^{-1} Y_{AB}^T V_A $

Substituindo o valor de $\small V_B$ na equação de $I_A$:

$\small I_A = Y_{AA} V_A - Y_{AB} Y_{BB}^{-1} Y_{AB}^T V_A $

Modificações na Matriz Admitância de Barra - Eliminação de Barras sem Fonte de Corrente

$\small I_A = Y_{AA} V_A - Y_{AB} Y_{BB}^{-1} Y_{AB}^T V_A $

Agrupando os termos:

$\small I_A = \underbrace {\left( {{Y_{AA}} - {Y_{AB}}Y_{BB}^{ - 1}Y_{AB}^T} \right)}_{{Y_A}}{V_A} $

$\small I_A = {{Y_A}}{V_A} $

A ordem da matriz $\small Y_A$ é a do número de barras com fonte de corrente.

Modificações na Matriz Admitância de Barra - Eliminação de Barras sem Fonte de Corrente - Exemplo 2.2.3

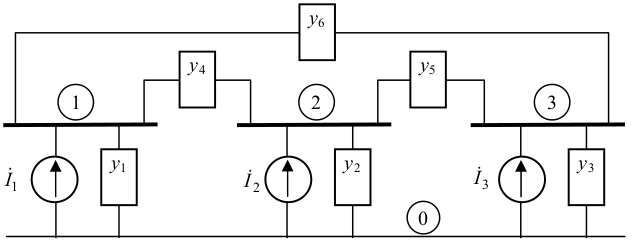
Eliminação de apenas uma barra do sistema de três barras da figura acima com $\small I_3 = 0$ (Eliminação de Kron).

Expressões das correntes:

$\small \left[ {\begin{array}{*{20}{c}} {{I_1}}\\ {{I_2}}\\ \cdots \\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{Y_{11}}}&{{Y_{12}}}& \vdots &{{Y_{13}}}\\ {{Y_{21}}}&{{Y_{22}}}& \vdots &{{Y_{23}}}\\ \cdots & \cdots & \cdots & \cdots \\ {{Y_{31}}}&{{Y_{32}}}& \vdots &{{Y_{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{V_2}}\\ \cdots \\ {{V_3}} \end{array}} \right]$

$\small {Y_A} = {{Y_{AA}} - {Y_{AB}}Y_{BB}^{ - 1}Y_{AB}^T} = \left[ {\begin{array}{*{20}{c}} {{Y_{11}}}&{{Y_{12}}}\\ {{Y_{21}}}&{{Y_{22}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{Y_{13}}}\\ {{Y_{23}}} \end{array}} \right]{\left[ {{Y_{33}}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{Y_{31}}}&{{Y_{32}}} \end{array}} \right]$

$\small {Y_A} = \left[ {\begin{array}{*{20}{c}} {{Y_{11}} - \frac{{{Y_{13}}{Y_{31}}}}{{{Y_{33}}}}}&{{Y_{12}} - \frac{{{Y_{13}}{Y_{32}}}}{{{Y_{33}}}}}\\ {{Y_{21}} - \frac{{{Y_{23}}{Y_{31}}}}{{{Y_{33}}}}}&{{Y_{22}} - \frac{{{Y_{23}}{Y_{32}}}}{{{Y_{33}}}}} \end{array}} \right]$

$\small {Y_A} = \left[ {\begin{array}{*{20}{c}} {{Y'_{11}} }&{{Y'_{12}} }\\ {{Y'_{21}} }&{{Y'_{22}} } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{Y_{11}} - \frac{{{Y_{13}}{Y_{31}}}}{{{Y_{33}}}}}&{{Y_{12}} - \frac{{{Y_{13}}{Y_{32}}}}{{{Y_{33}}}}}\\ {{Y_{21}} - \frac{{{Y_{23}}{Y_{31}}}}{{{Y_{33}}}}}&{{Y_{22}} - \frac{{{Y_{23}}{Y_{32}}}}{{{Y_{33}}}}} \end{array}} \right]$

Esta matriz representa um sistema equivalente ao sistema de três barras, agora com dimensão 2x2. Colocando-se de forma escalar, tem-se que a eliminação da barra $\small n$ é:

$\small Y{'_{ij}} = {Y_{ij}} - \frac{{{Y_{in}}{Y_{nj}}}}{{{Y_{nn}}}}$

A anterior expressão corresponde à chamada eliminação de Kron.

Para maior eficiência computacional, deve-se evitar a inversão da matriz $\small Y_{BB}$ . O procedimento é, então, o de eliminar uma barra por vez, aplicando-se a eliminação de Kron tantas vezes quanto o número de barras a serem eliminadas.

A partir de $Y_A$ pode se desenhar o circuito equivalente. No exemplo, têm-se agora duas barras, mostradas na figura a seguir, onde os elementos da nova matriz $\small Y_{\rm{Barra}}$, de dimensão 2×2, são:

$\small Y'_{11} = y'_1 + y'_3$, $\small Y'_{22} = y'_2 + y'_3$, $\small Y'_{12} = Y'_{21} = −y'_3$

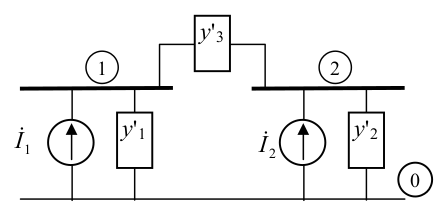
Modificações na Matriz Admitância de Barra - Eliminação de Barras sem Fonte de Corrente - Exemplo 2.2.4

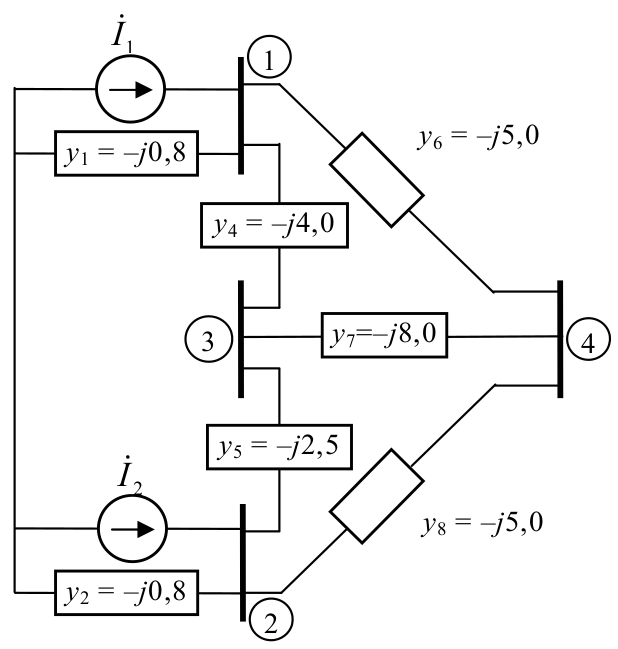
Eliminar as barras 3 e 4 do sistema da figura acima. Desenhar o circuito equivalente.

Expressão matricial das correntes:

$\small I = Y_{\rm{Barra}} V$

Matriz admitância de barra:

$\small Y_{\rm{Barra}} = \left[ {\begin{array}{*{20}{c}} { - j9,8}&{0,0}&{j4,0}& \vdots &{j5,0}\\ {0,0}&{ - j8,3}&{j2,5}& \vdots &{j5,0}\\ {j4,0}&{j2,5}&{ - j14,5}& \vdots &{j8,0}\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ {j5,0}&{j5,0}&{j8,0}& \vdots &{ - j18,0} \end{array}} \right]$

Eliminação da barra 4:

$\tiny Y_{\rm{Barra}} = \left[ {\begin{array}{*{20}{c}} { - j9,8}&{0,0}&{j4,0}& \vdots &{j5,0}\\ {0,0}&{ - j8,3}&{j2,5}& \vdots &{j5,0}\\ {j4,0}&{j2,5}&{ - j14,5}& \vdots &{j8,0}\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ {j5,0}&{j5,0}&{j8,0}& \vdots &{ - j18,0} \end{array}} \right]$

$\scriptsize Y{'_{ij}} = {Y_{ij}} - \frac{{{Y_{in}}{Y_{nj}}}}{{{Y_{nn}}}}$

$\scriptsize Y{'_{11}} = {-j9,8} - \frac{{{j5,0} \times {j5,0}}}{{{-j18,0}}} = -j8,41$; $\scriptsize Y{'_{12}} = Y{'_{21}} = {0,0} - \frac{{{j5,0} \times {j5,0}}}{{{-j18,0}}} = j1,39$

$\scriptsize Y{'_{13}} = Y{'_{31}} = {j4,0} - \frac{{{j5,0} \times {j8,0}}}{{{-j18,0}}} = j6,22$; $\scriptsize Y{'_{22}} = {-j8,3} - \frac{{{j5,0} \times {j5,0}}}{{{-j18,0}}} = -j6,91$

$\scriptsize Y{'_{23}} = Y{'_{32}} = {j2,5} - \frac{{{j5,0} \times {j8,0}}}{{{-j18,0}}} = j4,72$; $\scriptsize Y{'_{33}} = {-j14,5} - \frac{{{j8,0} \times {j8,0}}}{{{-j18,0}}} = -j10,94$

Após a eliminação da barra 4, a matriz $\small Y_{\rm{Barra}}$ fica:

$\small {Y_{{\rm{Barra}}}} = \left[ {\begin{array}{*{20}{c}} { - j8,41}&{j1,39}& \vdots &{j6,22}\\ {j1,39}&{ - j6,92}& \vdots &{j4,72}\\ \cdots & \cdots & \cdots & \cdots \\ {j6,22}&{j4,72}& \vdots &{ - j10,94} \end{array}} \right]$

Eliminação da barra 3:

$\scriptsize Y{'_{ij}} = {Y_{ij}} - \frac{{{Y_{in}}{Y_{nj}}}}{{{Y_{nn}}}}$

$\scriptsize Y{'_{11}} = {-j8,41} - \frac{{{j6,22} \times {j6,22}}}{{{-j10,94}}} = -j4,87$

$\scriptsize Y{'_{12}} = Y{'_{21}} = {j1,39} - \frac{{{j6,22} \times {j4,72}}}{{{-j10,94}}} = j4,07$

$\scriptsize Y{'_{22}} = {-j6,91} - \frac{{{j4,72} \times {j4,72}}}{{{-j10,94}}} = -j4,87$

Após a eliminação das barras 4 e 3, a matriz $\small Y_{\rm{Barra}}$ fica:

$\small {Y_{{\rm{Barra}}}} = \left[ {\begin{array}{*{20}{c}} { - j4,87}&{j4,07}\\ {j4,07}&{ - j4,87} \end{array}} \right]$

Na seguinte figura, apresenta-se o sistema de duas barras após eliminação das barras 4 e 3:

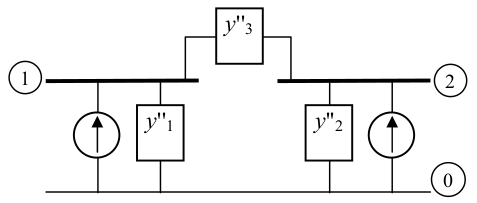
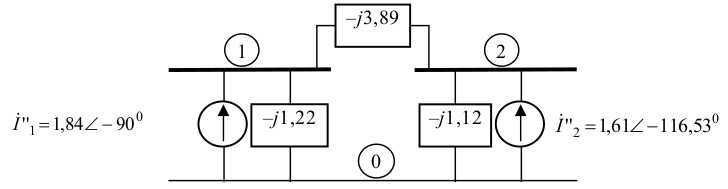
Para calcular os valores dos elementos do circuito da figura acima, basta aplicar as regras de construção da matriz $\small Y_{\rm{Barra}}$ e resolver o sistema. Assim, têm-se as seguintes expressões:

$\scriptsize Y''_{{\rm{Barra}},11} = {y''_{1}} + {y''_{3}} = - j4,87$

$\scriptsize Y''_{{\rm{Barra}},22} = {y''_{2}} + {y''_{3}} = - j4,87$

$\scriptsize Y''_{{\rm{Barra}},12} = Y''_{{\rm{Barra}},21} = - {y''_{3}} = j4,07$

$\scriptsize Y''_{{\rm{Barra}},11} = {y''_{1}} + {y''_{3}} = - j4,87$

$\scriptsize Y''_{{\rm{Barra}},22} = {y''_{2}} + {y''_{3}} = - j4,87$

$\scriptsize Y''_{{\rm{Barra}},12} = Y''_{{\rm{Barra}},21} = - {y''_{3}} = j4,07$

Resolvendo o sistema anterior:

$\scriptsize y''_{3} = - j4,87$

$\scriptsize y''_{1} = y''_{2} = - j4,87 + j4,07 = -j0,80$

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

A eliminação de uma barra onde existe fonte de corrente é semelhante à eliminação de Gauss.
Este método também vale quando não existe fonte de corrente na barra eliminada, sendo a fonte de corrente nula um caso particular.
A eliminação de Gauss consiste em transformar a matriz do sistema em uma matriz triangular superior. Com isto, encontra-se o valor de uma variável e, por substituição, todas as demais variáveis.
Quando da eliminação de barra com fonte de corrente pode ocorrer que uma barra, originalmente sem fonte, fique com fonte.

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

A eliminação de Gauss consiste de duas etapas:

Etapa 1: Normalização da primeira equação.

Etapa 2: Eliminação da variável pivotada nas demais equações.

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

Seja o sistema $\small I = Y_{\rm{Barra}} V $ de dimensão $3\times3$, escrito na forma estendida, apresentada a seguir:

$\small I_3 = Y_{33} V_3 + Y_{31} V_1 + Y_{32} V_2$

$\small I_1 = Y_{13} V_3 + Y_{11} V_1 + Y_{12} V_2$

$\small I_2 = Y_{23} V_3 + Y_{21} V_1 + Y_{22} V_2$

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

Etapa 1: Normalização da primeira equação. Dividindo-se a primeira linha por $\small Y_{33}$ e mantendo as outras linhas inalteradas:

$\small L_1: \frac{I_3}{Y_{33}} = 1 \times V_3 + \frac{Y_{31}}{Y_{33}} V_1 + \frac{Y_{32}}{Y_{33}} V_2$

$\small L_2: I_1 = Y_{13} V_3 + Y_{11} V_1 + Y_{12} V_2$

$\small L_3: I_2 = Y_{23} V_3 + Y_{21} V_1 + Y_{22} V_2$

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

Etapa 2: Eliminação da variável pivotada nas demais equações. Eliminação da variável pivotada $\small V_3$ ($\small L'_i$ substitui a linha $\small i$, $\small L_i$):

$\small L_1: \frac{I_3}{Y_{33}} = 1 \times V_3 + \frac{Y_{31}}{Y_{33}} V_1 + \frac{Y_{32}}{Y_{33}} V_2$

$\small L_2: I_1 = Y_{13} V_3 + Y_{11} V_1 + Y_{12} V_2$

$\small L_3: I_2 = Y_{23} V_3 + Y_{21} V_1 + Y_{22} V_2$

$\small L'_2 = L_2 - Y_{13} \times L_1$

$\small L'_3 = L_3 - Y_{23} \times L_1$

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

$\small L_1: \frac{I_3}{Y_{33}} = 1 \times V_3 + \frac{Y_{31}}{Y_{33}} V_1 + \frac{Y_{32}}{Y_{33}} V_2$

$\small L_2: I_1 = Y_{13} V_3 + Y_{11} V_1 + Y_{12} V_2$

$\small L_3: I_2 = Y_{23} V_3 + Y_{21} V_1 + Y_{22} V_2$

$\small L'_2 = L_2 - Y_{13} \times L_1$

$\small L'_2: I'_1 = I_1 - \frac{Y_{13} I_{3}}{Y_{33}} = 0 \times V_3 + \left({ Y_{11} - \frac{Y_{13} Y_{31}}{Y_{33}} }\right) V_1 + \left({ Y_{12} - \frac{Y_{13} Y_{32}}{Y_{33}} }\right) V_2 $

$\small L'_2: I'_1 = \left({ Y_{11} - \frac{Y_{13} Y_{31}}{Y_{33}} }\right) V_1 + \left({ Y_{12} - \frac{Y_{13} Y_{32}}{Y_{33}} }\right) V_2 $

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

$\small L_1: \frac{I_3}{Y_{33}} = 1 \times V_3 + \frac{Y_{31}}{Y_{33}} V_1 + \frac{Y_{32}}{Y_{33}} V_2$

$\small L_2: I_1 = Y_{13} V_3 + Y_{11} V_1 + Y_{12} V_2$

$\small L_3: I_2 = Y_{23} V_3 + Y_{21} V_1 + Y_{22} V_2$

$\small L'_3 = L_3 - Y_{23} \times L_1$

$\small L'_3: I'_2 = I_2 - \frac{Y_{23} I_{3}}{Y_{33}} = 0 \times V_3 + \left({ Y_{21} - \frac{Y_{23} Y_{31}}{Y_{33}} }\right) V_1 + \left({ Y_{22} - \frac{Y_{23} Y_{32}}{Y_{33}} }\right) V_2 $

$\small L'_3: I'_2 = \left({ Y_{21} - \frac{Y_{23} Y_{31}}{Y_{33}} }\right) V_1 + \left({ Y_{22} - \frac{Y_{23} Y_{32}}{Y_{33}} }\right) V_2 $

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

$\small L'_2: I'_1 = \left({ Y_{11} - \frac{Y_{13} Y_{31}}{Y_{33}} }\right) V_1 + \left({ Y_{12} - \frac{Y_{13} Y_{32}}{Y_{33}} }\right) V_2 $

$\small L'_3: I'_2 = \left({ Y_{21} - \frac{Y_{23} Y_{31}}{Y_{33}} }\right) V_1 + \left({ Y_{22} - \frac{Y_{23} Y_{32}}{Y_{33}} }\right) V_2 $

O sistema fica então reduzido a:

$\small Y'_{11} V_1 + Y'_{12} V_2 = I'_1 $

$\small Y'_{21} V_1 + Y'_{22} V_2 = I'_2 $

A formação do termo $\small Y'_{ij}$ é a mesma da redução de Kron para a eliminação da barra $\small n$, ou seja:

$\small Y{'_{ij}} = {Y_{ij}} - \frac{{{Y_{in}}{Y_{nj}}}}{{{Y_{nn}}}}$

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente

$\small Y{'_{ij}} = {Y_{ij}} - \frac{{{Y_{in}}{Y_{nj}}}}{{{Y_{nn}}}}$

A formação das novas correntes injetadas, para a eliminação da barra $\small n$, é dada por:

$\small I{'_{i}} = {I_{i}} - \frac{{{Y_{in}}{I_{n}}}}{{{Y_{nn}}}}$

Modificações na Matriz Admitância de Barra - Eliminação de Barras com Fonte de Corrente - Exemplo 2.2.5

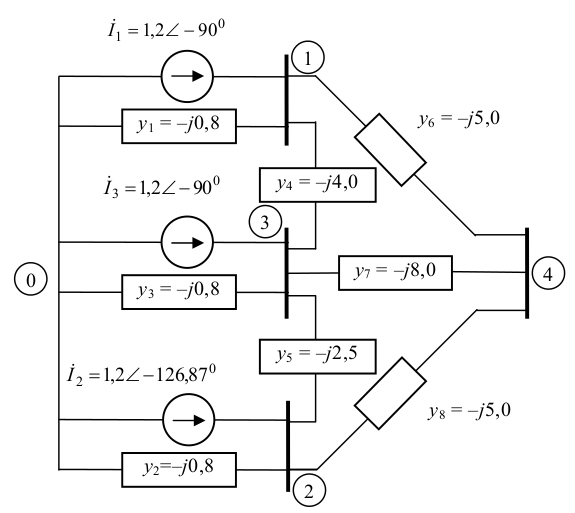
Eliminar as barras 3 e 4 do sistema da figura acima. Desenhar o circuito equivalente.

Expressão matricial das correntes:

$\small I = Y_{\rm{Barra}} V$

$\small \left[ {\begin{array}{*{20}{c}} {1,2\angle - 90^{\circ}}\\ {1,2\angle - 126,87^{\circ}}\\ {1,2\angle - 90^{\circ}}\\ {0,0} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - j9,8}&{0,0}&{j4,0}&{j5,0}\\ {0,0}&{ - j8,3}&{j2,5}&{j5,0}\\ {j4,0}&{j2,5}&{ - j15,3}&{j8,0}\\ {j5,0}&{j5,0}&{j8,0}&{ - j18,0} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{V_2}}\\ {{V_3}}\\ {{V_4}} \end{array}} \right]$

Eliminação da barra 4:

$\tiny \left[ {\begin{array}{*{20}{c}} {1,2\angle - 90^{\circ}}\\ {1,2\angle - 126,87^{\circ}}\\ {1,2\angle - 90^{\circ}}\\ {0,0} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - j9,8}&{0,0}&{j4,0}&{j5,0}\\ {0,0}&{ - j8,3}&{j2,5}&{j5,0}\\ {j4,0}&{j2,5}&{ - j15,3}&{j8,0}\\ {j5,0}&{j5,0}&{j8,0}&{ - j18,0} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{V_2}}\\ {{V_3}}\\ {{V_4}} \end{array}} \right]$

$\scriptsize Y{'_{ij}} = {Y_{ij}} - \frac{{{Y_{in}}{Y_{nj}}}}{{{Y_{nn}}}}$

$\scriptsize Y{'_{11}} = {-j9,8} - \frac{{{j5,0} \times {j5,0}}}{{{-j18,0}}} = -j8,41$; $\scriptsize Y{'_{12}} = Y{'_{21}} = {0,0} - \frac{{{j5,0} \times {j5,0}}}{{{-j18,0}}} = j1,39$

$\scriptsize Y{'_{13}} = Y{'_{31}} = {j4,0} - \frac{{{j5,0} \times {j8,0}}}{{{-j18,0}}} = j6,22$; $\scriptsize Y{'_{22}} = {-j8,3} - \frac{{{j5,0} \times {j5,0}}}{{{-j18,0}}} = -j6,91$

$\scriptsize Y{'_{23}} = Y{'_{32}} = {j2,5} - \frac{{{j5,0} \times {j8,0}}}{{{-j18,0}}} = j4,72$; $\scriptsize Y{'_{33}} = {-j15,3} - \frac{{{j8,0} \times {j8,0}}}{{{-j18,0}}} = -j11,74$

Após a eliminação da barra 4, o sistema fica:

$\small \left[ {\begin{array}{*{20}{c}} {1,2\angle - 90^{\circ}}\\ {1,2\angle - 126,87^{\circ}}\\ {1,2\angle - 90^{\circ}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - j8,41}&{j1,39}&{j6,22}\\ {j1,39}&{ - j6,91}&{j4,72}\\ {j6,22}&{j4,72}&{ - j11,74} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{V_2}}\\ {{V_3}} \end{array}} \right]$

Eliminação da barra 3:

$\scriptsize Y{'_{ij}} = {Y_{ij}} - \frac{{{Y_{in}}{Y_{nj}}}}{{{Y_{nn}}}}$

$\scriptsize Y{'_{11}} = {-j8,41} - \frac{{{j6,22} \times {j6,22}}}{{{-j11,74}}} = -j5,11$

$\scriptsize Y{'_{12}} = Y{'_{21}} = {j1,39} - \frac{{{j6,22} \times {j4,72}}}{{{-j11,74}}} = j3,89$

$\scriptsize Y{'_{22}} = {-j6,91} - \frac{{{j4,72} \times {j4,72}}}{{{-j11,74}}} = -j5,01$

$\scriptsize I{'_{1}} = 1,2 \angle -90^{\circ} - \frac{{{j6,22} \times 1,2 \angle -90^{\circ}}}{{{-j11,74}}} = 1,84 \angle -90^{\circ}$

$\scriptsize I{'_{2}} = 1,2 \angle -126,87^{\circ} - \frac{{{j4,72} \times 1,2 \angle -90^{\circ}}}{{{-j11,74}}} = 1,61 \angle -116,53^{\circ}$

Após a eliminação das barras 4 e 3, o sistema fica:

$\small \left[ {\begin{array}{*{20}{c}} {1,84\angle - 90^{\circ}}\\ {1,61\angle - 116,53^{\circ}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - j5,11}&{j3,89}\\ {j3,89}&{ - j5,01} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{V_2}} \end{array}} \right]$

Na seguinte figura, apresenta-se o sistema de duas barras após eliminação das barras 4 e 3:

Análise de Sistemas de Energia Elétrica

Universidade Federal do Espírito Santo

Departamento de Engenharia Elétrica

Prof. Augusto César Rueda Medina / CT-XI, Sala 27 / augusto.rueda@ufes.br